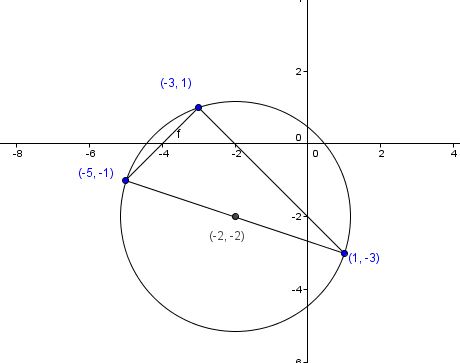
We could solve this with some Algebra....but ...it's messy...a Geometric solution is actually easier
(1, -3), (-3, 1) and (-5, -1).
Find the midpoint and slope between the first two points
Midpoint [ (1 - 3)/ 2 , (-3 + 1)/2)] = (-2/2, -2/2) = (-1, -1)
Slope = [ 1 - - 3] / [ -3 - 1] = [ 4/ -4] = -1
And the negative reciprocal of the slope = 1
So.....using the midpoint and the negative reciprocal slope, the equation of the line with this slope and passing through the midpoint is y = 1 (x - - 1) - 1 ⇒ y = x + 1 - 1 ⇒ y = x (1)
Now using any of the other two points [ I'll use (1, -3) and (-5, - 1) ] we want to do he same thing
Midpoint [ ( -5 + 1) / 2 , (-3 -1 ) / 2 ] = [ ( -4/ 2 ), ( -4/2) ] = (-2, -2)
Slope between these points = [ - 1 - - 3] / [ -5 - 1 ] = [ 2/-6] = (-1/3)
And the negative reciprocal slope is 3
So...using this slope and the midpoint....we can write the equation of the line as
y = 3(x - - 2) -2 ⇒ y = 3x + 6 - 2 ⇒ y = 3x + 4 (2)
Find the x coordinate of the intersection of (1) and (2)....this will be he x coordinate of the center of the circle
x = 3x + 4
-2x = 4
x = - 2
And using y = x
The y coordinate of this intersection is -2
So the center of this circle is (-2 , - 2)
Snd the distance from this center to any of the points is the radius....so ...using the point (1, -3)....the radius^2 is
(-2 - 1)^2 + ( -2 - -3)^2 =
(-3)^2 + (1)^2 =
10
So.....the equation of the circle passing through these 3 points is
(x + 2)^2 + (y + 2)^2 = 10
Here's the graph: