Hello Guest!
The original equation: \(x^2-y^2=51+xy\) (*)
Factorise the L.H.S: \((x-y)(x+y)=51+xy\)
The R.H.S will always be positive, as \(x>0,y>0 \implies xy>0\)
So, the L.H.S has to be always positive, hence, \(x>y\) is a must condition.
We can rewrite (*) as follows:
\(x(x-y)=51+y^2\) (1)
\(y(y-x)=x^2-51\) (2)
Observe (2): we know x>y but notice (y-x)... This is negative!
Hence, L.H.S of (2) is negative, and so R.H.S must also be negative.
That is, \(x^2-51 <0 \implies x \le 7\) (**)
So, x could be any of the following:
x: 2,3,4,5,6,7
We can, from here, try to solve the quadratic in (1) using each x, but a quicker way is as follows:
Ok, let's solve for y in (1):
\(y^2+xy-x^2+51=0\)
Quadratic formula:
\(y=-\frac{x\pm\sqrt{5x^2-204}}{2}\)
Observe: \(5x^2-204\ge 0 \implies x\ge7\) (***)
Look at (**) and (***)
Thus, x has to be 7 (To satisfy both inequalities.)
But, substituting x=7 in (3) does not give an integer value of y.
This means, there does not exist integer pairs (x,y) such that (*) is satisfied.
Therefore, 0 pairs.
Also, Wolframalpha gives no integer solutions:
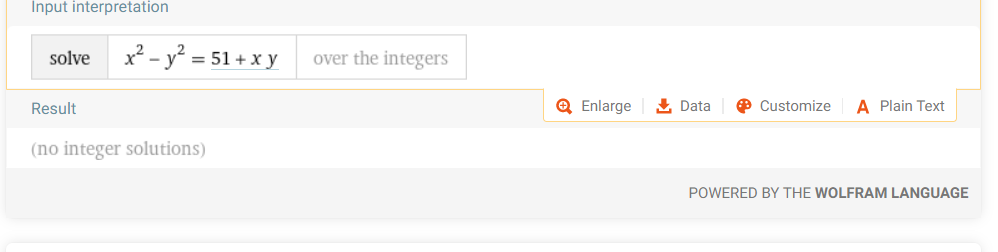
Hope this helped!