There is a formula to find the area of a triangle for this exact situation. I will use a picture to illustrate it:

Source: http://maths.nayland.school.nz/Year_12/AS_2.4_Trigonometry/Images/Pinboard_posters/ScreenShot043.gif
In the diagram above, if we know the lengths of 2 sides of a triangle and the measure of the included angle, then the area of the triangle can be found using the formula of \(A_\triangle=\frac{1}{2}ab\sin C\). Now, let's apply the formula!
| \(A_\triangle=\frac{1}{2}ab\sin C\) | Plug in the the side lengths as a and b (order is immaterial) and the measure of the included angle as C. |
| \(A_\triangle=\frac{1}{2}(1)(1)\sin 30^{\circ}\) | Let's simplify the sin of 30 degrees. You may already be aware that\(\sin 30^{\circ}=0.5\). |
| \(A_\triangle=\frac{1}{2}(1)(1)(0.5)\) | If you multiply a number by 1, the number is itself. |
| \(A_\triangle=\frac{1}{2}(0.5)\) | (1/2)*0.5=1/4, or 0.25. |
| \(A_\triangle=\frac{1}{4}units^2=0.25units^2\) | |
Hectictar's method is perfectly executed, but this equation is also factorable. How do I know? There is a universal test that determines if a quadratic is factorable. It is the following:
If \(\sqrt{b^2-4ac}\in\mathbb{Q}\hspace{1mm}\text{and}\sqrt{b^2-4ac}\geq0\), then the quadratic is factorable. In other words, the standard form of a quadratic equation is \(ax^2+bx+c\). If you apply the rule above and get a rational number (integers and decimals that terminate or repeat) and is greater than or equal to 0, then the quadratic is factorable. Let's try it:
\(4a^2-10a+6=0\)
Before, we start, let's determine our a's, b's, and c's. Our a is the coefficient of the quadratic term. In this case, that is 4. OUr b is the coefficient in front of the linear term, which is -10. Make sure to include the sign when doing this calculation. Our c is our constant term, which is 6. Let's apply the rule and see if this equation is factorable:
| \(\sqrt{b^2-4ac}\in\mathbb{Q}\hspace{1mm}\text{and}\sqrt{b^2-4ac}\geq0\) | Check to see if the condition is true by plugging in the appropriate values for a, b, and c. |
| \(\sqrt{(-10)^2-4(4)(6)}\) | Simplify inside the radical first. |
| \(\sqrt{100-96}\) | |
| \(\sqrt{4}\) | |
| \(2\) | This meets the condition of being apart of the set of rational numbers and being greater than or equal to 0. |
Great! Now that we have determined that this quadratic can be factored, let's factor it! I'll use a picture to demonstrate what I am doing:

Our job is to find 2 factors that both multiply to get -24 and add to get -10. If you toy with the numbers for some time, you will eventually figure this out:
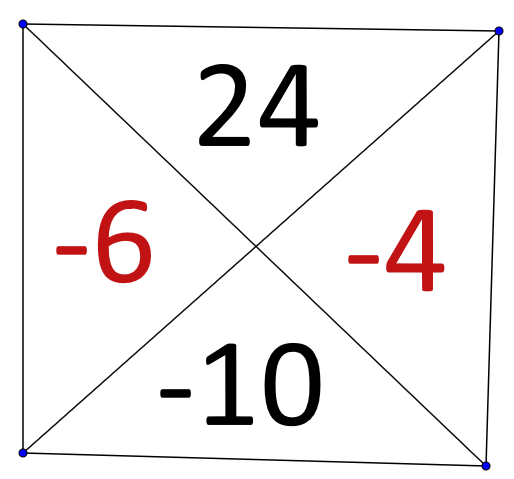
Now that we have figured out which two numbers satisfy the above problem, let's split the b-term:
| \(4a^2-10a+6=0\) | Split the -10a into -6a and -4a. | ||
| \(4a^2-4a-6a+6=0\) | Solve this by grouping. | ||
| \((4a^2-4a)+(-6a+6)=0\) | Factor out the GCF of both in the parentheses. | ||
| \(4a(a-1)-6(a-1)=0\) | Now, use the rule that \(a*c\pm b*c=(a\pm b)(c)\). | ||
| \((4a-6)(a-1)=0\) | In the first set of parentheses, you can factor out a GCF of 2 from the equation, so let's do that. | ||
| \(2(2a-3)(a-1)=0\) | Set both factors equal to zero and solve each set by using the zero-product theorem. | ||
| Add the constants in both equations. | ||
| |||
| |||
Therefore, your solution set is the following:
\(a_1=\frac{3}{2}\)
\(a_2=1\)
Now, you are done!
Let's let everyone jump in! Since hecticlar didn't do #4, I will do number 4.
\(x^4+3x^2+3=1\)
| \(x^4+3x^2+3=1\) | Subtract 1 on both sides. | ||
| \(x^4+3x^2+2=0\) | This expression is factorable. Think: What number multiplies to get 2 and add to get 3. That's right! 2 and 1! | ||
| \((x^2+1)(x^2+2)=0\) | Set both factors equal to 0 and solve. | ||
| |||
| Take the square root of both sides. | ||
|
Now, let's simplify both solutions:
\(x=\pm\sqrt{-1}=\pm i\)
\(x=\pm\sqrt{-2}=\pm\sqrt{-1*2}=\pm i\sqrt{2}\)
Those are your solutions all done and dusted!
| 1. | x2 = x - 1 | ||
| x2 - x + 1 = 0 | |||
| x = ( 1 ± √[ 1 - 4] )/ 2 | |||
| x = ( 1 ± √3 i ) / 2 | There are no real solutions for x . | ||
| 2. | √[ x + 5] - 2 = 6 | ||
| √[ x + 5] = 8 | |||
| x + 5 = 82 | |||
| x = 82 - 5 | |||
| x = 59 |
3. \(\, \ \, \ \, (\sqrt[3]{3}+\sqrt[3]{2})(\sqrt[3]{4}-\sqrt[3]{6}+\sqrt[3]{9}) \\ =(\sqrt[3]3)(\sqrt[3]{4})-(\sqrt[3]3)(\sqrt[3]{6})+(\sqrt[3]3)(\sqrt[3]{9}) + (\sqrt[3]{2})(\sqrt[3]{4})-(\sqrt[3]{2})(\sqrt[3]{6})+(\sqrt[3]{2})(\sqrt[3]{9}) \\ =\sqrt[3]{12}-\sqrt[3]{18}+\sqrt[3]{27} + \sqrt[3]{8}-\sqrt[3]{12}+\sqrt[3]{18} \\ =\sqrt[3]{27} + \sqrt[3]{8} \\ =3+2\\ =5\)
5. \(\, \ \, \ \, \sqrt{10000}-\sqrt{81}+\sqrt{81} \\ =\sqrt{10000} \\ =\sqrt{10^4} \\ =10^2 \\ =100\)
6. \(\frac{8}{x}=x+\frac1{x} \\~\\ 8=x^2+1 \\~\\ 7=x^2 \\ x=\pm\sqrt{7} \\ \text{ The smallest value is -sqrt(7) .}\)
.