I think the points on the graph are:
(0, negative 4) and (pi over 2, 0) and (pi, 4) and (3 pi over 2, 0 ) and (2 pi, negative 4)
There is the point (0, -4) . So, when x = 0 , y = -4 .
There is the point (\(\frac{\pi}{2}\), 0) . So, when x = \(\frac{\pi}{2}\) , y = 0 .
average rate of change = \(\frac{\text{change in y}}{\text{change in x}}=\frac{-4 - 0}{0 - \frac{\pi}{2}}=\frac{4}{\frac{\pi}{2}}=4\cdot\frac2{\pi}=\frac8{\pi}\)
Here's a graph.
I know why the second answer is incorrect, but mathemathh made a mistake that is very easy to overlook.
If TP = 7, then TO can be 7 or 11 to make the triangle isosceles.
If TP = 5, then TO can 5 or 11
Stop right there, though! Your logic is correct, but TO cannot be 5! Why? Triangles have certain properties that they must adhere to for a triangle to exist. One such theorem is called the triangle inequality theorem. It states that the sum of the lengths of two different sides is greater than the remaining third side.
| \(5+5>11\) | |
| \(10>11\) | This is false; 10 is not greater than 11, which means that a triangle with sidelengths 5,5,and 11 cannot exist. |
The other side length possibilities adhere to this restriction, thankfully. Now, add 7 and 11. \(17+11=18\)
.Another way to solve this problem is to use what the hint suggests-- the triangle inequality theorem.
The triangle inequality theorem states that the sum of the lengths of two different sides of a triangle is greater than the third remaining side. Here is a picture that demonstrates this theorem. It might be easier to understand that way:
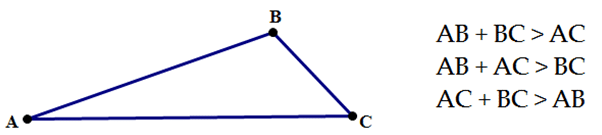
Let's apply this to the current problem. Here is a picture to reference as I solve:

Knowing the triangle inequality theorem, let's just worry about 1 triangle at a time. Let's worry about \(\triangle ABC\). Let's use the theorem to determine the possible lengths that \(\overline{AC}\) can be:
| \(AB+BC>AC\) | \(AB+AC>BC\) | \(AC+BC>AB\) | Replace the known values into these inequalities and solve. |
| \(3+6>AC\) | \(3+AC>6\) | \(AC+6>3\) | |
| \(9>AC\) | \(AC>3\) | \(AC>-3\) | |
With so many solutions, sometimes it easier me to sketch a graph of all the solutions and figure out where the solutions overlap. Here is a picture of the number line graph:

Where is the area of overlap? The area of overlap is from 3 to 9. Therefore, we can express the possible lengths of AC as the following compound inequality: \(3 . We aren't done yet! We now have to consider the other triangle, \(\triangle ACD\). Again, we will have to consider and use the triangle inequality theorem again:
| \(AD+DC>AC\) | \(DC+AC>AD\) | \(AC+AD>DC\) | Yet again, plug in the known values. |
| \(4+4>AC\) | \(4+AC>4\) | \(AC+4>4\) | Solve. |
| \(8>AC\) | \(AC>0\) | \(AC>0\) | |
For this one, you could use a number line graph again, but I will just use logic to figure out the set of possible lengths AC can be in this case. In two of our inequalities, it was determined that \(AC>0\). If \(8>AC\), or, as I like to think of it, \(AC<8\), this means that the compound inequality for AC in this case is \(0 . Now, let's look at the restriction we placed on AC before.
\(3
\(0
AC has to comply to both restrictions because it is in both triangles, which means that the final compound inequality is
\(3 . Therefore, the only possible integers are 4, 5, 6, and 7.
Bam! Done!