All Answers 358080 Answers

Thanks, hectictar......these often throw me.....!!!!

The given intersection points lie on  y = h(x)  and  y = j(x)  .

For example...since  (8, 12)  is an intersection point....   12 = h(8)   and   12 = j(8)

When  x = 4  ,     h(2x)    =    h(2(4))    =    h(8)    =    12    =    y

When  x = 4  ,     2j(x)     =    2j(4)       =    2(6)    =    12    =    y

So... (4, 12)  is a point on  y = h(2x)  and on  y = 2j(x)  .

4 + 12  =  16

Sorry that this isn't a very good explanation.....If it doesn't make sense, it might help to try different numbers for  x  , such as 1, 2, or 6...to see why they don't work.  

0.375    write as a fraction

375 / 1000     divide numerator/denominator by 5 

75 / 200         divide by 5 again

15 /40            divide by 5 once more

 3 / 8

(x - 3) / 5  =   1  - x / 3          

To clear the fractions, multiply through by the common denominator of 3,5  =15

15 (x - 3) / 5  = 15  - 15x / 3

3(x - 3)  = 15 - 5x      simplify

3x - 9  = 15 - 5x       add 5x, 9 to both sides

8x  = 24            divide both sides by 8

x  = 3

Don't worry.....if you passed Algebra and Pre-Cal pretty easily, Calculus won't give you any trouble.....my experience is that it's not the Calculus that gives people trouble in Calc I, it's the Algebra....[ believe it, or not !!!]

\( $f(x)=\frac{2x}{x^2-5x-14}$\)

Factoring the denominator, we have

2x / [ (x - 7)  ( x + 2) ]

Note that x = 7   or x  = -2   make the denominator undefined.....so these are the vertical asymptotes

And since the degree of the poynominal in the numerator is one less than that of the denominator, we will have a horizontal asymptote at y = 0

So.....the sum of the asymptotes  is  =  7 - 2 + 0   = 5

I get something a little different, atroshus.....

Refer to the following image :

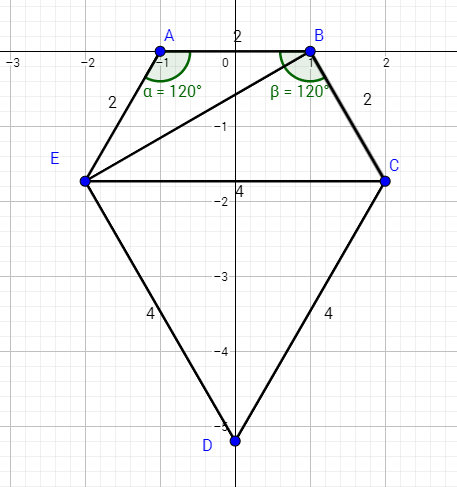
Note that the area of triangle EAB  = (1/2)(2)(2)sin120  = 2 * √3 / 2  =  √3

And this triangle is isosceles......so angle ABE  = 30°

But since angle ABC  = 120°.....then triangle EBC is a right triangle with angle EBC = 90°

And since EB is a transversal cutting parallel segments AB and EC....then angle ABE  = angle BEC = 30°....then triangle EBC is a 30 - 60 - 90 right triangle with angle BCE = 60°

And since BC  = 2 and is opposite the 30° angle......then the hypotenuse EC is twice this = 4

So......the area of triangle EBC  = (1/2)(2)(4)sin 60  = 4 * √3/2  =  2 √3

And triangle CDE is equilateral with an area = (1/2)(4)(4) sin60  = 8 √3 / 2  = 4√3

So the total area of ABCDE  =  [ √3 + 2√3 + 4√3 ] =  7√3 units^2

Let \[ f(x) = \begin{cases} -x^2 & \text{if } x \geq 0,\\ x+8& \text{if } x <0. \end{cases} \]Compute $f(f(f(f(f(1))))).$

\(\text{Let } \left[ f(x) = \begin{cases} -x^2 & \text{if } x \geq 0,\\ x+8& \text{if } x <0. \end{cases} \right] \\ \text{Compute } f(f(f(f(f(1))))). \)

\(\begin{array}{|llcll|} \hline x=1 \quad & f(1) = -1^2 &=& -1 & | \quad (x\ge 0) \\ x=-1 \quad & f(-1) = -1+8 &=& 7 & | \quad (x \lt 0) \\ x=7 \quad & f(7) = -7^2 &=& -49 & | \quad (x\ge 0) \\ x=-49 \quad & f(-49) = -49+8 &=& -41 & | \quad (x \lt 0) \\ x=-41 \quad & f(-41) = -41+8 &=& -33 & | \quad (x \lt 0) \\ \hline \end{array} \)

\(f(f(f(f(f(1))))) = -33\)

After 3 hours of trigging on it, i came up the the answer 11 also

it used to be 2 but after common core took over.  if you were to put 

2, then 1 & 1 would feel belittled and discriminated against.  causing 

a lawsuit against all numbers 2 and above. so for political correctness,

the answer is 11 

We have that

(a + 1)^2  + (6a)^2  = (6a + 1)^2    simplify

a^2 + 2a+ 1 + 36a^2   =  36a^2 + 12a + 1

a^2  + 2a  = 12a 

a^2  - 10a  = 0

a ( a - 10)  = 0     

So....a  = 0  (reject )  or      a  = 10  which is correct

I got 11sqrt3 but it wasn't correct

=================================

half hexagon at the bottom = 3sqrt3

((3sqrt3/2)*2^2)/2

top triangle = 8sqrt3

edge length 2= long diagonal 4 << length from E to C

draw point halfway E to C to create point F

EF=CF=2

pythagorean theorem: DF= 2sqrt3

area of top triangle = DF*4 = 8sqrt3

add up= 10sqrt3

Just do as much as you can to go to college and live a happy life.

-quote from Ghosty.

Thank you.

Yes, I hope this helped!

Your exam must be extremely hard to have 1+1 in it.

It took the #-Ghosty Calculator-# hours to solve that.

Thanks! This helped a lot! 

Now I can pass my math exam with flying colours :D

well answered ghosty

1+1 is surely 11.

There is no way that 2 would be the answer.

Let's use a calculator to check.

{{

#-Ghosty Calculator-#

{Type: 1+1=?}

Processing...

Loading...

**{Click here for answer >>> ^(Answer)^

:You have clicked the answer key. Please wait...:

Loading...

Answer: 11

Thank you for using  # -Ghosty Calculator-#

We hope you have a wonderful day.

}}

To get the area of a rhombus, you need to multiply the diagonals and divide the result by 2. 

So you multiply 24 and 10 and divide the result by 2.

24*10 = 240.

240/2 = 120.

The area of the rhombus is 120 square units.

what ever equation you put in to get that number just put it in here

https://www.symbolab.com/solver/radical-equation-calculator

im sure they can give you a better number to work with

Multiple outcomes..? I don't quite Get what you ment.. x, y, and z does not have to be the same number.. therefor different names, bit yet they could be the exact same in your equation.

And no, x, y and z will not give you multiple outcomes of the same, let's say, x.

x is x is your equation and that won't change

say x = 5457912602

       z = 1

       y = 10612134962648607623

( 5457912602 - 5457912601 ) = ( Z ) = ( 10612134962648607623 + 10612134962648607622 )

then IT would be 1 = 1 = 1

or x is 1, z is 1, and y is 1

then they would all be different

Do you mean 1 7/10? This is 1.7. 

Well, in xy-wy  = t,  you know that xy and wy both have y in them. (Yeah, that's not really a good explanation -_-)

So you can make that into: y(x-w) = t. Because if you distribute y to (x-w), the result is the same as the original. 

Now, we have y(x-w) = t.

We need to isolate y to solve for y.

So divided both sides by (x-w) to isolate y.

you get y = t/(x-w)

And that's the answer.

Correct me if I am wrong. 

Do you mean 1.1818181818... by 1.18 repeating? If so, the fraction would be 1 2/11, or 13/11. Here is a great site for converting decimals to fractions. https://www.calculatorsoup.com/calculators/math/decimal-to-fraction-calculator.php

Sorry...didn't understand the question properly. Deleting answer...

Well, to solve for m, you need to isolate it. 

First subtract 4m to both sides so that you only have m on one side.

But you might realize that by subtracting 4m to both sides, m is gone.

What's left is -4 = 0.

Now that -4 is certainly not equal to 0.

So there is no solution.

There is no real number that can satisfy this equation.