The question asks for "80% of 55."
"Of" is an indicator for the multiplication indicator. You can replace it. We have now changed the question to \(80\% *55\). Now, let's evaluate it!
| \(80\% *55\) | In general, \(a\%=\frac{a}{100}\). |
| \(\frac{80}{100}*\frac{55}{1}\) | Let's simplify 80/100 to simplest terms by realizing that the numerator and denominator have a greatest common factor of 20. |
| \(\frac{4}{5}*\frac{55}{1}\) | To faciliate the computational process even more, notice that 5 and 55 havea GCF of 5. |
| \(\frac{4}{1}*\frac{11}{1}\) | Now, do the multiplication. |
| \(44\) | |
Therefore, 80% of 55 is 44.
Here's a diagram to reference as I solve. I made it myself.
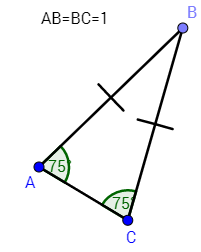
Despite that it is not noted on my diagram, \(m\angle B=30^{\circ}\), according to the given info. We already have enough information to solve for the area of the triangle.
In a triangle, if the length of 2 sides and measure of the included angle are known, then we can use the following formula to determine the area of the triangle. It is the following:
\(A_{\triangle}=\frac{1}{2}ab*\sin C\)
a = 1 side length of triangle
b = Another side length of the triangle
C = measure of the included angle
Now that we know this formula, just substitute into it.
| \(A_{\triangle}=\frac{1}{2}ab*\sin C\) | Plug in the appropriate values for a, b, and C. |
| \(A_{\triangle}=\frac{1}{2}*1*1*\sin (30)\) | You may have remembered that \(\sin(30)=\frac{1}{2}\). |
| \(A_{\triangle}=\frac{1}{2}*1*1*\frac{1}{2}\) | Of course, 1 mulriplied by a number is itself. |
| \(A_{\triangle}=\frac{1}{2}*\frac{1}{2}\) | Simplify this. |
| \(A_{\triangle}=\frac{1}{4}units^2=0.25units^2\) | Of course, do not forget to include the units! |
If I had to take a guess, I would say that one of the millennium prize problems set by the Clay Mathematics Institute at the beginning of the millennium. Only one has been solved thus far.
Out of those, the easiest to understand is P versus NP.
Click here to redirect yourself to the corresponding wikipedia page.
Before we start, let's define a few terms.
Odds is the ratio of the probability that an event can occur to the probability that an event cannot occur. Here is the formula in algabraic notation, if it makes it easier to understand.
\(\text{Odds}=\frac{p}{1-p}\)
p = probability
Probability is the ratio of the ways an event suits a condition to the number of possible outcomes.
\(p=\frac{\text{# of events}}{\text{# of outcomes}}\)
p = probability
Knowing this, we can answer all the questions up to 11.
8)
There are 3 primary colors in the colored cube, and this allows us to calculate the odds.
\(\text{Odds}=\frac{{\frac{1}{2}}}{1-\frac{1}{2}}=\frac{\frac{1}{2}}{\frac{1}{2}}=1:1\)
9)
Let's calculate the probability of not rolling a blue or purple. If we wanted to roll a blue or purple, the probability would be \(\frac{2}{6}=\frac{1}{3}\). The probability of that event not occuring is \(1-p\). Therefore, \(1-\frac{1}{3}=\frac{3}{3}-\frac{1}{3}=\frac{2}{3}\). Now, let's determine the odds.
| \(\text{Odds}=\frac{\frac{2}{3}}{1-\frac{2}{3}}\) | Simplify the denominator |
| \(1-\frac{2}{3}=\frac{3}{3}-\frac{2}{3}=\frac{1}{3}\) | |
| \(\text{Odds}=\frac{\frac{2}{3}}{\frac{1}{3}}\) | Multiply by \(\frac{3}{3}\) to eliminate the ugly denominator. |
| \(\text{Odds}=\frac{2}{3}*\frac{3}{1}=\frac{6}{3}=2:1\) | |
10)
There are 3 primary colors on the cube, which means that the probability is \(\frac{3}{6}=\frac{1}{2}\)
11) The probability of an event not occuring is represented by \(1-p\), so this means that \(1-\frac{1}{6}\) is the probability. Now, just simplify this.
\(1-\frac{1}{6}=\frac{6}{6}-\frac{5}{6}=\frac{1}{6}\)
.