All Answers 358080 Answers

Hello! That's quite an interesting expression you got there of \((a-7)^2-2(a-7)(a+7)+a+7\). Let's simplify it the we can.

Therefore, \((a-7)^2-2(a-7)(a+7)+a+7=-a^2-13a+154\).

For A, I think I know why it is not working properly. You appear to have done everything correctly, so I presume that there is a silly computational error. 

1. Determine the Midpoint of Both Coordinates

The midpoint is the average of both x- and y- coordinates. In algabraic terms, the formula is \(\left(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}\right)\). Let's use it! You used this formula correctly, as I can tell. For completeness, I'll calculate it also.

2. Determine Slope (or Gradient) of the Segment

This also has a formula, luckily, and all we have to do is plug the coordinates in. It is \(m=\frac{y_2-y_1}{x_2-x_1}\), where m is the slope of the segment. Let's just use the formual to determine the slope.

This is not the slope of the perpendicular bisector but rather the slope of the original 2 segments.

3. Determine The Slope of Perpendicular Bisector

A line that is perpendicular to a segment has a slope that is opposite and reciprocal to the slope of the original segment. What does that mean? Well, let's deal with the current slope as its example of \(-\frac{1}{3}\).

I find doing the reciprocal of a number first is generally easier, but the order in which you do the next steps do not matter. In general, the reciprocal of a number follows tthe following rule of \(a\Rightarrow\frac{1}{a}\). Let's apply that now with our slope. \(-\frac{1}{3}\Rightarrow-\frac{1}{\frac{1}{3}}=-3\)

Now, find the opposite. To do this, use the rule that \(a\Rightarrow-a\). \(-3\Rightarrow3\).

Therefore, \(3\) is the slope of the perpendicular bisector. 

If you are interested, here is another method to obtain the slope of the perpendicular bisector. If you take the original slope of the segment and multiply it by the slope of the perpendicular bisector, you will get -1. Let's see this in action!

Look at that! you get the same answer. 

4. Use Point-Slope Form

There are 2 methods again to get to the final equation of the slope, but I generally like point-slope form for some reason, but I will demonstrate both to you, so that you can choose your method. Point-slope form is the following:

\(y-y_1=m(x-x_1)\) where \((x_1,y_1)\) is a point on said segment or line and m is the slope of said segment or line. We know what segment is on this perpendicular bisector; we already calculated it. The perpendicular bisector is a segment that both intersects a segment at its midpoint and at a perpendicular angle. We have already calculated the midpoint of BC, which is \(\left(\frac{9}{2},\frac{5}{2}\right)\). We also know the slope, which is 3. Since we have all that information, let's plug it in!

This is the equation of the perpendicular bisector. I'm not sure where you went wrong, unfortunately, but it seems to me that it is probably some silly computational error. That's all. 

Another method of doing this is using the slope-intercept form from the beginning. Let's see how that would work:

Hopefully, this helped to find the segment that is the perpendicular bisector. 

Now, it is time to do B. Thankfully, this will not be as time-consuming as generating this repsonse has taken me hours. The point you want me to identify is called the circumcenter of the triangle. it is the point located at the center of a circle such that circle contains all the points in a triangle. The circumcenter of a triangle can be found by finding the intersection of 2 of the perpendicular bisectors! Let's do that. We already know 2 lines and their respective equations. They are \(y=3x-11\) and \(y+2x=4\). Let's set up a system of equations.

{ \(y=3x-11\)

{ \(y+2x=4\)

I will use substitution in this case as we already know what y equals.

Now, plug in x into one of the equations. I think that equation 1 will be easier, so I will use that!

Therefore, the circumcenter of the triangle is \((3,-2)\). 

I cannot access that ???

What does this mean??

5%7.75

Hello my friend. I just wanted to know why you are asking this to everyone. 

Two distinct points $A$ and $B$ are on a circle with center at $O$, and point $P$ is outside the circle such that $\overline{PA}$ and $\overline{PB}$ are tangent to the circle. Find $AB$ if $PA = 12$ and the radius of the circle is 9.

20^3/50*pi = 502.6548245743669182

Three circles of radius 1 are externally tangent to each other and internally tangent to a larger circle.
What is the radius of the large circle?
Express your answer as a common fraction in simplest radical form.

Let Radius of the larger circle = R.
Let Radius of the three circles = r = 1.

Let Area of the triangle ABC = \(A_{ABC}\)
Let Area of the triangle AOB = \( A_{AOB}\)

Let AC = CB = BA = 2r
Let AO = OB = R-r

\(\mathbf{A_{ABC} = \ ?}\)

\(\begin{array}{|lrcll|} \hline (\text{Heron}) & s &=& \frac{2r+2r+2r}{2} \\ & &=& 3r \\ & A_{ABC}^2 &=& s(s-2r)(s-2r)(s-2r) \\ & A_{ABC}^2 &=& s(s-2r)^3 \quad & | \quad s = 3r \\ & A_{ABC}^2 &=& 3r(3r -2r)^3 \\ & A_{ABC}^2 &=& 3rr^3 \\ & A_{ABC}^2 &=& 3r^4 \\ & A_{ABC} &=& r^2 \sqrt{3} \\ \hline \end{array}\)

\(\mathbf{A_{AOB} = \ ?} \)

\(\begin{array}{|lrcll|} \hline & A_{AOB} &=& \frac{A_{ABC}}{3} \\ (1) & A_{AOB} &=& \frac{r^2 \sqrt{3}}{3} \\ \hline \end{array}\)

\(\mathbf{(\text{Heron})\ A_{AOB} = \ ?}\)

\(\begin{array}{|rcll|} \hline (\text{Heron}) & s &=& \frac{2r+(R-r)+(R-r)}{2} \\ & s &=& \frac{2R}{2} \\ & s &=& R \\ & A_{AOB}^2 &=& s(s-2r)[s-(R-r)][s-(R-r)] \quad & | \quad s = R \\ & A_{AOB}^2 &=& R(R-2r)[R-R+r)][R-R+r] \\ & A_{AOB}^2 &=& R(R-2r)r^2 \\ (2) & A_{AOB} &=&r\sqrt{R(R-2r)} \\ \hline \end{array}\)

(1) = (2)

\(\begin{array}{|rcll|} \hline \frac{r^2 \sqrt{3}}{3} &=& r\sqrt{R(R-2r)} \\ \frac{r \sqrt{3}}{3} &=& \sqrt{R(R-2r)} \quad & | \quad \text{square both sides}\\ \frac{r^2}{3} &=& R(R-2r) \\ R^2-2rR -\frac{r^2}{3} &=& 0 \quad & | \quad \cdot 3 \\ 3R^2-6rR - r^2 &=& 0 \\ \\ R &=& \frac{6r \pm \sqrt{36r^2-4\cdot 3\cdot (-r^2) } }{2\cdot 3} \\ R &=& \frac{6r \pm \sqrt{36r^2+12r^2 } }{6} \\ R &=& \frac{6r \pm \sqrt{48r^2 } }{6} \\ R &=& \frac{6r \pm 4r\sqrt{3} }{6} \\ R &=& r \pm \frac23 r \sqrt{3} \quad & | \quad R \gt 0 \\ R &=& r + \frac23 r \sqrt{3} \quad & | \quad r = 1 \\ \mathbf{R} & \mathbf{=} & \mathbf{1 + \frac23 \sqrt{3}} \\ \hline \end{array}\)

And the answer is 512

Let a_1, a_2, . . . , a_{10} be an arithmetic sequence. If a_1 + a_3 + a_5 + a_7 + a_9 = 17 and a_2 + a_4 + a_6 + a_8 + a_{10} = 15, then find a_1.

Letting d be the common difference between terms, note that we can write the terms of the first sum as

[a1] + [a1 + 2d] + [a1 + 4d ] + [ a1 + 6d ] + [a1 + 8d ]  = 17

Simplify as .... 5a1 + 20d  = 17    (1)

And for the sum of the second series, we can write the terms as

[a1 + d ] + [a1 + 3d ] + [ a1 + 5d ] + [ a1 + 7d] + [ a1 + 9d]  = 15

Simplify as ....  5a1 + 25d  = 15   (2) 

Subtract  (1)  from (2)  and we have that

5d  = -2

d  =  -2/5

And using (1) to solve for  a1

5a1 + 20 (-2/5) = 17

5a1  - 8  =  17

5a1  = 25

a1  = 25/5 = 5

Check this with (2)

5(5) + 25(-2/5)  =

25 - 10  =

15

A certain 300-term geometric sequence has first term 1337 and common ratio of -1/2. How many terms of this sequence are greater than 1?

Note that the terms that are positive are the odd terms ... 

And each positive term  can  actually be written as

1337 (1/4)^n   where n is the nth positive term  after the first one

And we want to find this

1337 (1/4)^n > 1

(1/4)^n  > 1/1337       take the log of each side

log (1/4)^n > log (1/1337)

And we can write......[remember to reverse the sign since  log (1/4)  is negative ]

n < log (1/1337)/log(1/4)  

n < 5.19

So....there are 5 terms [after the first one] > 1   .....which gives 6 terms total

Proof ....the 10th term after the first one - the 6th positive one-  is     1337(-1/2)^(10) ≈ 1.03

And the 12th term after the first one - the 7th positive one -  is  1337(-1/2)^(12) ≈ .326

Laverne starts counting out loud by 5's. She starts with 7. As Laverne counts, Shirley sums the numbers Laverne says. When the sum finally exceeds 5000, Shirley runs screaming from the room. What number did Laverne last say before Shirley flees?

Note that we have this series

                                                                 5n + 7 - 7 +1  

7, 12, 17, 22, 27, 32.....

Note that the first term is 7  and the last is  5(n-1) + 7 =  5n + 2

And the sum  can  be represented as  [ first term + last term ] * number of terms / 2

So we  need to solve this

[ 7 + 5n + 2] * n / 2  > 5000        simplify this

[5n + 9 ] * n > 10000

5n^2 + 9n > 10000

5n^2 + 9n - 10000 > 0

The positive solution for this is when  n > 43.83

Note that the 43rd term 5(43) + 2  = 217 

And the sum of the first 43 terms is  [ 7 + 217] * 43/2  = 4816 

And  the  44th term is 222

And this will cause the sum to be greater than 5000

So....before  Shirley flees, the last number Laverne says is 217

log₄ x  =  -3

In exponential form, this is...

4^-3  =  x

1 / ( 4³ )  =  x

1 / 64  =  x

May be faster ways to do this, but look at the following:

Let the centers of two of the circles lie at (1,0)  and (-1,0)

So....to find the center of the third circle let it be located at  (0,y)   

And by the Pythagorean Theorem we have

y = sqrt [ GD^2 - HD^2 ]

y= sqrt [ 2^2 - 1^2]  =  sqrt (3)

So the center of the top circle =  ( 0, sqrt (3) )  call this point  G

Let point E be the center of the circle.....and it will be located at (0, c )

Now let B be  the point tangent to the top circle and the leftmost circle

And its coordinates will be  the midpoint of  CG =   [ -1/2 , sqrt (3)/2 )

Let A be the intersection of the apex of the top circle and  the y axis.......and its coordinates  are

(0, GA + GH )  =  ( 0, 1 + sqrt (3) ) 

And....by similar triangles

(BF) / FD  = HE /HD

(sqrt [(3)/2] )   / (3/ 2)  =  HE / 1    →   HE  =  sqrt (3)/3

So....the radius of the large circle  = [AH - HE]  =  EA =

[1 +  sqrt (3)] -   [sqrt (3)/3]  =

1 + (2/3) sqrt (3) 

No prob  !!!!

Thanks CPhil!

0  will not be in the range of either fiunction

The first one is a ceiling function....this means that it returns the least integer that is ≥ to f(x)

When   -2 < x < -1          the range is  [2, infinity )

When   x ≥ -1          the range is   1

The second is a floor function....this means that it returns the greatest integer ≤ to f(x)

When    -3 < x < -2    the range  is ( -infinity, -2 ]

When  x ≤ -3              the range is  -1

So......  the integer 0  is not in the range

The sum of two sixth degree polynomials can result in a cubic polynomial. Write an example of this.

(x⁶ + x⁵ + x⁴ + x³ + x² + x + 1)  +  (-x⁶ - x⁵ - x⁴)   =   x³ + x² + x + 1

OA is a radius = 9

Because  OAP  is a right angle, OP  = sqrt ( PA^2 + OA^2)  = sqrt (12^2 + 9^2)  = 

sqrt (225)  =  15

Let AB intersect OP at R

And triangles  OPA and OAR  are similar

So

PA / OP  =  AR / OA

12 / 15  =  AR / 9

AR  = 108/15  =  36/5

And AR  = (1/2) AB  ...so

AB  = 2 (AR) =  2(36/5)   =  72/5

Also, thumbs up me!

To achieve the desired result, she needs five heads in a row.....

And the probability of five heads in a row is   (1/2)⁵  =  1 / 32

Solve for x: log(x) = -6 

Cancel logarithms by taking exp of both sides:

 x = 1/e^6 

When squaring a number that ends in "5", such as this example, there is a very simple and beautiful trick that you can use to get the answer very quickly. This is what you do: 35 x 35 = Multiply the two "5's" by each other and you, of course, get: 5 x 5 = 25. The next digit is "3" and multiply it by the next higher digit or "4" in this case and, of course, you would get: 3 x 4 =12. Then put the two results together and you have: 1,225 !. So, 45 x 45 =2,025 and 55 x 55 =3,025, and 75 x 75 =5,625...and so on.

\(35*35=1225\)

I believe you want an easier method to work out problems like these where you square a number. Here is an idea for you.

\(35^2=?\)

When you square a number, this is a trick you can use! Round the number to the nearest multiple of 10. In this case, that is 30. Now, go up by the distance you went down. In this example, you went down by 5 to get to 30. Now, go up 5 to get to 40. Now multiply them together.

This should be much simpler now. \(30*40=1200\). All you need to do now is to add the square of the distance. In this case, it is \(5^2=25\).

\(1200+25=1225\)

That's much easier, don't you think? In fact, this is usually so easy that you may be able to do it mentally.

But why does it work? Well, that is actually easier to explan than you may think. Let's call the number we want to square A. Let's call the distance we want to go up and down d. Therefore, we get the following equation:

This means that no matter what distance you pick, you will eventually make it the original number squared. That's pretty cool!

For the purposes of this problem, I will assume "when you are given one of the sides and an angle" means an angle other than the right angle. Another assumption I am making is that one of the given side lengths is not the hypotenuse as I doubt you would ask for the length of the hypotenuse if you already knew its side length. If these conditions are true, there are still 2 possibilities. I have created a diagram for both scenarios. Here they are:

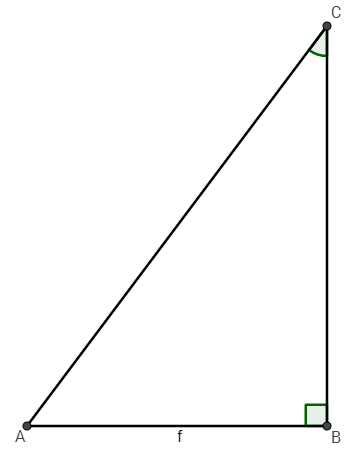
Let's assume that \(AB=6\) and \(m\angle C=35^{\circ}\). Now, let's "solve" the triangle. "Solving" the triangle means to figure out all the missing side lengths and angle measures. Let's start with the easy one first. You can use the triangle sum theorem to figure out what the measure of the angle located at vertex A:
 

The next part requires the knowledge of right-triangle trigonometry. Let's review that quickly. I understand that 

\(\frac{\sin \textcolor{\green}\alpha}{1}=\frac{\textcolor{red}{\text{opposite}}}{\textcolor{blue}{\text{hypotenuse}}}\)

\(\frac{\cos \textcolor{green}{\alpha}}{1}=\frac{\textcolor{red}{\text{adjacent}}}{\textcolor{blue}{\text{hypotenuse}}}\)

\(\frac{\tan \textcolor{green}{\alpha}}{1}=\frac{\textcolor{red}{\text{opposite}}}{\textcolor{blue}{\text{adjacent}}}\)

Since we know that \(AB=6\) and \(m\angle C=35^{\circ}\), we should use the sine function to calculate the length of the hypotenuse and the tangent function for the angle adjacent to the known angle. Let's solve for the hypotenuse!

Now, let's solve for the other side length. This time, we will need the tangent function.

We have solved the triangle because we have found all the missing side lengths and angle measures. However, there is 1 scenario that we have not covered yet. However, the process is the same. Here is the diagram, with AB=5 and \(m\angle A=25^{\circ}\). You will notice that this is different that the first diagram. 

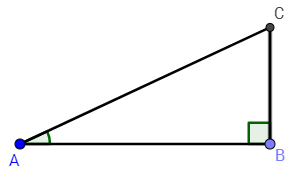
Let's find the easy one again: the measure of the angle of C:

Oh wait! Now, this looks the exact same as the 1st triangle because we know the measure of the angle across from the known side length. Therefore, to solve this triangle, you would use the exact same process as done above.