All Answers 356759 Answers

the answer is 67.5961107239166535

It is the common "Modulus" we want, not the biggest common "divisor". That will not satisfy the two equations. Try it!.

Since   the first value we're given is, - 4   we want to look for the correct function to plug this into

Notice that the last function is only good when x > 1......so that's not the one we want

The second function is only good when  x > -4     [and  ≤ 1 ]    so....we don't want that one, either

So....the first one says it's good when  x  is less than or equal to  - 4.....so that's the one we want

So    ....puting  -4  into x^2  we get    (-4)   =  16

Then...we want to choose the correct function when x  = 4

This is obviously the last one   since it's good when  x > 1

So...plugging  4  into √ x....we get  √ 4    = 2

The biggest factor they have in common is 2^2 * 331 = 1324.

We don't have a direct method of finding the Modulus, but we can proceed as follows:

If the Modulus =M
If the quotient =Q for the first and =q for the second, then we have:
MQ + 199 = 57,131.................(1), and:
Mq + 67   =37,139...................(2) 
Will ignore the Modulus "M" for now and re-write the two equations as:
Q =57,131 - 199 =56,932.........(3)
q =37,139 - 67    =37,072.........(4). Will factor (3) and (4) as follows:
56,932 = 2^2 * 43 * 331, and:
37,072 = 2^4 * 7 * 331
From the above factorization, we can readily see that the biggest factor they have in common is =331. Then we have:
57,131 mod 331 = 199, and
37,139 mod 331 = 67. And that satisfies both equations.

\(f(x)=4x+7\)

so if we plug in 4 we get

\((4*4)+7=23\)

23 is the answer

no we will not do your homework for you...

dude your math is wrong

no problem and your welcome and i am happy to help

Dallas  =  1 x 10^6

Los Angeles  = 3 times Dallas  =   3 [ 1 x 10^6]  =   3 x 10^6

Pittsburgh / Dallas   =    [ 3 x 10^5 ]  /  [ 1 x 10^6]  = 3 / 10  that of Dallas

guest.... Thanks for pointing out my earlier mistake  !!!!!

2sin (2x)

__________    =     5

1 - sin^2 (x)

2sin(x)cos(x)   

___________  =    5

cos^2(x)

2sin (x)

______         =     5

cos (x)

2tan(x)  =  5              divide both sides by 2

tan (x)   = 5/2    = 1.25

 Area = (side)^2

So......

√ Area   = side

-2x^2 + 242  = 0      divide through by  -2

x^2 - 121   =  0       add 121 to both sides

x^2  = 121   take positive / negative  roots

x  = ±√121

x  = ±11

_________((__((__((__((__((
_________ ▌__▌__▌__▌__ ▌
______▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓
_____ {~*~*~ ★★★ ~*~*~}
_____ {~*╔╦╗────────*~}
_____ {~*║╩╠═╦═╦═╦╦╗*~}
_____ {~*║╦║╬║╬║╬║║║*~}
_____ {~*╚╩╩╩╣╔╣╔╬╗║*~}
_____ {~*────╚╝╚╝╚═╝*~}
_____ {~*~*~ ★★★ ~*~*~}
______▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓
______ ≡•≡•≡•≡•≡•≡•≡•≡•≡
__▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒
__{~*~*~*~* ★★★ *~*~*~*~}
__{~* ╔═╦╗─╔╗╔╗─╔╗────*~}
__{~* ║╚╠╬╦╣╚╣╚╦╝╠═╦╦╗*~}
__{~* ║╔║║╔╣╔╣║║╬║╬║║║*~}
__{~* ╚═╩╩╝╚═╩╩╩═╩╩╬╗║*~}
__{~* ─────────────╚═╝*~}
__{~*~*~*~* ★★★ *~*~*~*~}
__▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒
__≡≡•≡•≡•≡•≡•≡•≡•≡≡•≡•≡≡
__▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒
▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓
_ ▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼_
▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓
████████████████████████
_______▀████████████▀.o•°★°•o. 
___________▀██████▀★ Do I Smell ★
_____________ ████ ☻ Birthday Cake? ☻
_____________ ████____()_()_.-”"-.,/)
_____________ ████____; . . `; -._ , `)
___________▄▄████▄▄( o_ ) __,) `-._)

Hope you get a lot of presents and have a lot of people over for your Birthday! ^^

╱╱╱╭━━━╮╱╱╱╱╭┳━━━┳╮
╱╱╱┃╭━╮┃╱╱╱╱┃┃╭━╮┃┃
╱╱╱┃╰━╯┣━━┳━╯┃┃╱╰┫┃╭━━┳━━┳━━┳━━┳━━╮
╭━━┫╭╮╭┫┃━┫╭╮┃┃╭━┫┃┃╭╮┃━━┫━━┫┃━┫━━┫
╰━━┫┃┃╰┫┃━┫╰╯┃╰┻━┃╰┫╭╮┣━━┣━━┃┃━╋━━┃
╱╱╱╰╯╰━┻━━┻━━┻━━━┻━┻╯╰┻━━┻━━┻━━┻━━╯

happy birthday

happy birthday

Once again it is not displaying properly only this time it is the LaTex that is not displaying correctly  

Jeff123,

It would be really nice if you would comment on my answers. I think my answers are correct but this technique is quite new to me.  If you have any reason to think the answers are incorrect (like maybe the probability answer is printed in your text book) it would be really nice if you share what you know. 

QUESTION 2

(2) Three points are selected randomly on the circumference of a circle. What is the probability that the triangle formed by these three points contains the center of the circle?

I drew this picture in Geogebra. The real thing is interactive and by playing with it I concluded that if all the angles of the triangle are acute then the centre will be included. 

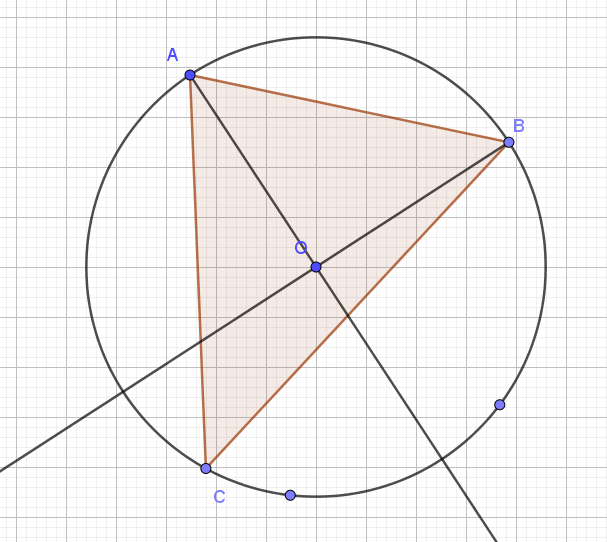
Now it is very similar to the first problem only maybe easier.  

Let the 3 angles be  x, 180-y  and y-x   

Where y>x and each of thes angles is acute.

\(0 x \qquad (3)\\ x<90\qquad (4)\\ 180-y<90\\ -y<-90\\y>90 \qquad (5)\\ y-x<90\\ y

Here is the Boolean contour map  so if y>x then the probability is 1/8

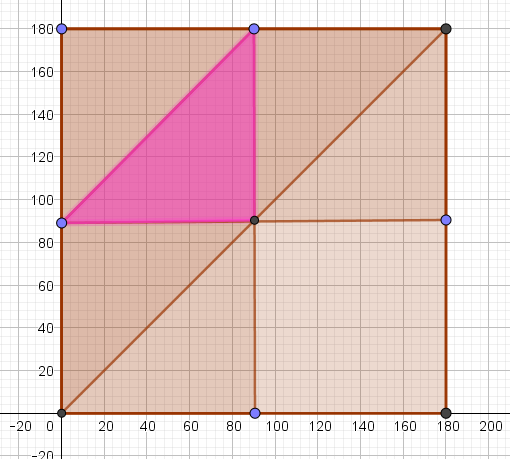
BUT if x>y then you have the inverse of this region. I mean this region reflected over  the line y=x

SO

It seems to me that the probability that the centre will be in the triangle is 1/4

happy birthday! \(do\)\(x^3=y(\frac{2o}{2})(\frac{\frac {\int {e}^{du}}{C}}{d})\)  \(l\sqrt{-1}ke\)\(3.14159265...\) ? (btw it says "do you like pie?")

Happy birthday !