All Answers 357307 Answers

Ahhh yes!! What was I thinking, that makes sense. 

Thanks 

tan^2 (x) * sin (x) - sin (x) / 3  = 0     get a common denominator

[ 3tan^2 (x) * sin (x) - sinx] / 3  = 0     mutiply both sides by 3

3tan^2 (x) * sin (x) - sin (x)  = 0        factor out sin(x)

sin (x)  [  3tan^2 ( x)  - 1]   =  0

We have two equations here.....either.......

sin (x)  = 0       and this happens at   0  and   pi 

Or

3tan^2 (x)  -  1   =  0       add 1 to both sides

3tan^2 (x)   =   1           divide both sides by 3

tan^(2) x  =  1/3            take both roots

tan (x)  =  1/√3      and this happens at  pi/6   and 7pi/6

And

tan (x)  =  -  1/√3   and this happens at  5pi/6  and 11pi/6

So.....the solutions are    0, pi/6, 5pi/6, pi, 7pi/6 and 11pi/6

I think I woud divide through by sin x  to get started.....

Ohh yeah Melody, she was VERY polite. All she said that if no one was monitoring him/her she would cuss me out. Well, that's polite. Excuse my misunderstanding (With SARCASM intended). 

 (x^2y-3)/[2-y^(-3) ] = 

(x^2y-3)/( 2 -  1 / y^3 )  =

( x^2y - 3) / [  (2y^3 - 1) /  y^3) ]

[ y^3 (x^2y - 3) ] / {2y^3 - 1)

[ x^2y^4 - 3y^3 ] / [ 2y^3 -1 ] 

We can't solve the second one for anything because we have to have an equation for that

If the blue square is  3.8 cm  by  3.8 cm ....

the area of the blue square   =   (3.8 cm)²   =   14.44 cm²

the area of the white square   =   (5 cm)²   =   25 cm²

the area of all four triangles   =   25 cm²  -  14.44 cm²   =   10.56 cm²

The four triangles are congruent,so..

the area of one triangle   =   10.56 cm² / 4   =   2.64 cm²

(1/2) * 3.8 cm * height  =  2.64 cm²

1.9 cm * height   =   2.64  cm²

height   =   2.64 / (1.9)  cm

height   ≈   1.389  cm

yknowwhat? after school im gonna bike over too 7-Eleven and buy me some donuts!!!!

i would love too but i dont have any 

A         

Off.      

fell

fat 

It's been a while since I've posted a math explanation...

Alright, you'll have to subtract those two equations, but you have to make one term (with variable) the same.

Let's allow both equations to have 3x. 

3x+2y=16 already has 3x inside, so leave it alone.

So for x-y=-3 to have 3x, you multiply 3 to every term in that equation. 

3x-21=-9.

Let's subtract now.

        3x-3y=-9

-

        3x+2y=16

________________

         -5y    = -25

So we have -5y = -25

Divide both sides by -5 and you get y=5.

Plug 5 for y in any equation to get x. I'll use the first one. 

x-5=-3

x = 2

So x=2, y=5.

Uh...thank you. Have a nice day too. 

thanks you have a good day ok

Wow that's really optimistic.

Well then. Why don't you eat some donuts, donut?

CPhill, thank you very much

Yep, Heureka....your approach is much better  !!!!

Triangle $ABC$ is inscribed in equilateral triangle $PQR$, as shown.

If $PC = 3$, $BP = CQ = 2$, and $\angle ACB = 90^\circ$, then compute $AQ$.

Let u = BC

Let v = CA

Let w = AB

Let x = AQ

Let PQ = PR = RQ = 5

Let BR = PR - BP $= 5-2=3$

Let AR = RQ - AQ $= 5 - x$

Using the Law of Cosines:

$\begin{array}{|rcll|} \hline u^2 &=& BP^2 + PC^2 - 2\cdot BP \cdot PC\cdot \cos(60^{\circ}) \quad & | \quad 2\cdot \cos(60^{\circ}) = 2\cdot \frac12 = 1 \\ u^2 &=& BP^2 + PC^2 - BP \cdot PC \quad & | \quad BP =2 \quad PC = 3 \\ u^2 &=& 2^2 + 3^2 - 2 \cdot 3 \\ \mathbf{u^2} & \mathbf{=} & \mathbf{2^2 + 3^2 - 6} \\ \hline \end{array}$

Using the Law of Cosines again:

$\begin{array}{|rcll|} \hline v^2 &=& CQ^2 + AQ^2 - 2\cdot CQ \cdot AQ\cdot \cos(60^{\circ}) \quad & | \quad 2\cdot \cos(60^{\circ}) = 2\cdot \frac12 = 1 \\ v^2 &=& CQ^2 + AQ^2 - CQ \cdot AQ \quad & | \quad CQ =2 \quad AQ = x \\ \mathbf{v^2} & \mathbf{=} & \mathbf{2^2 + x^2 - 2x} \\ \hline \end{array}$

Using the Law of Cosines again:

$\begin{array}{|rcll|} \hline w^2 &=& BR^2 + AR^2 - 2\cdot BR \cdot AR\cdot \cos(60^{\circ}) \quad & | \quad 2\cdot \cos(60^{\circ}) = 2\cdot \frac12 = 1 \\ w^2 &=& BR^2 + AR^2 - BR \cdot AR \quad & | \quad BR =3 \quad AR = 5-x \\ \mathbf{w^2} & \mathbf{=} & \mathbf{3^2 + (5-x)^2 - 3 \cdot (5-x)} \\ \hline \end{array}$

Using Pythagoras' theorem:

$\begin{array}{|rcll|} \hline u^2+v^2&=& w^2 \\ (2^2 + 3^2 - 6) + (2^2 + x^2 - 2x) &=& 3^2 + (5-x)^2 - 3 \cdot (5-x) \\ 2^2 + \not{3^2} - 6 + 2^2 + x^2 - 2x &=& \not{3^2} + (5-x)^2 - 3 \cdot (5-x) \\ 2^2 - 6 + 2^2 + x^2 - 2x &=& (5-x)^2 - 3 \cdot (5-x) \\ 2 + x^2 - 2x &=& (5-x)^2 - 3 \cdot (5-x) \\ 2 + \not{x^2} - 2x &=& 25 - 10x + \not{x^2} -15+3x \\ 2 - 2x &=& 25 - 10x -15+3x \\ 2 - 2x &=& 10 - 7x \\ 5x &=& 8 \\ x &=& \frac85 \\ \mathbf{x} & \mathbf{=} & \mathbf{1.6} \\ \hline \end{array}$

AQ is 1.6

Look at the following diagram to get a feel for this :

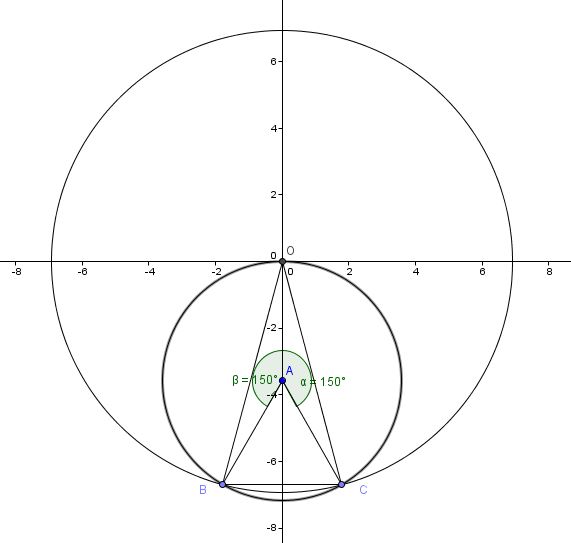
The  larger circle will have the equation

x^2 + y^2  = 48

Since  A will be the circumcenter for BOC.....then the distance from A to O will be the same distance as from A to B  and from A to C

And since ABC is equilateral, then BAC  = 60°

Then major angle  BAC  = 300°

And using symmetry, angle OAC  = 150°

But AO = AC....so...triangle  OAC is isosceles....   and angle AOC  = 15°

And since OC is a radius of the larger circle it equals √48

So......we can find a side of the equilateral triangle - AC - thusly

OC / sin (OAC) = AC/ sin (AOC)

√48 / sin (150)  =  AC / sin (15)

AC  =  √48sin (15) / sin (150)  = 

AC = √48   ( sin (45 -30) / (1/2) =

2√48 (sin45sin30 - sin30cos45) =

2√48 (√2√3 / 4   - √2 / 4)  =

√48/2 (√6 - √2 )  =

2√3 ( √6  - √2 )

√12 ( √6 - √2)  =

√72  - √24   =

6√2 - 2√6  (exact value)

Then  the equation for the circle with A as a center  passing through the vertices of BOC  is

x^2  +  (y^2 +6√2 - 2√6)^2  = ( 6√2 - 2√6)^2

And the area of equilateral triangle ABC  =  (√3 /4)s^2  =

(√3/4) (6√2 - 2√6)^2  =

(√3 / 4) ( √72 - √24)  =

(√3/ 4) ( 72  - 2 √(72*24) + 24) =

(√3/ 4) ( 96 - 2√1728)  =

(√3/ 4) (96 - 48√3)  =

12√3 ( 2 - √3)  =

24√3 - 36   units ^2   ≈  5.57  units^2