The steps are not too long-winded luckily. Unfortunately for Cphill, the 3 that precedes the argument is missing from Cphill's answer.
1) As Cphill mentioned, if \(f(x)\) is the original function, then \(f(x-6)\) translates the function 6 units rightward. The instructions specificially request for the answer with an equation of \(g(x)\) in terms of \(f(x)\), \(g(x)=f(x-6)\)
2) In the previous answer, we determined that \(g(x)=f(x-6)\), so we can use this information to solve for the current problem:
| \(g(x)=f(x-6)\\ f(x)=3(x-5)^2+9\) | \(f(x)=3(x-5)^2+9\) |
| \(f(x-6)=3[(x-6)-5]^2+9\) | |
| \(f(x-6)=3(x-11)^2+9\) | |
| \(g(x)=f(x-6)=3(x-11)^2+9\\ g(x)=3(x-11)^2+9\) |
3) If \(g(x)\) is translated 7 units downward to obtain \(j(x)\), then \(g(x)-7=j(x)\). Of course, the question asks for the equation to be in terms of f(x):
| \(j(x)=g(x)-7\) | Now, substitute g(x)=f(x-6). |
| \(j(x)=f(x-6)-7\) | |
4) Find j(x) in terms of x:
| \(j(x)=g(x)-7\) | We have determined previously that \(g(x)=3(x-11)^2+9\), so substitute that in. |
| \(j(x)=[3(x-11)^2+9]-7\) | Now, simplify. There is not much to do. |
| \(j(x)=3(x-11)^2+2\) | |
The second one was definitely much harder for me to come up with! Here is a picture that may be useful to reference as I solve:
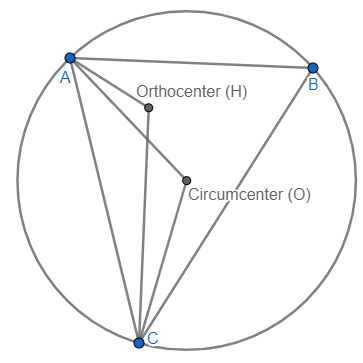
You will probably notice that I added a circle that inscribes the triangle. At its bost basic level, the circumcenter is a point that is equidistant from all the vertices of the triangle. The circumcenter is also the center of a triangle's circumcircle, which I have illustrated with the diagram above. Of course, we know that the sum of \(\angle AHC\) and \(\angle AOC\) is 240 by the given info. Notice that \(m\angle AOC=m\angle AHC\) because they both intercept the same arc. Therefore, we can solve for the angle of the circumcenter.
| \(m\angle AOC+m\angle AHC=240\) | Since we already established that \(m\angle AOC=m\angle AHC\), we can solve for the the central angle of the circle. |
| \(m\angle AOC+m\angle AOC=240\) | |
| \(2m\angle AOC=240\) | |
| \(m\angle AOC=120^\circ\) | There is no need to solve for the angle measure of the orthocenter; it is simply a waster of time. |
Notice that \(\angle ABC\) is an inscribed angle, which means that its measure is equal to half the measure of the central angle.
| \(\frac{1}{2}m\angle AOC=m\angle ABC\) | Use substitution here since we already know the measure of one of the angles. |
| \(\frac{1}{2}*120=m\angle ABC\) | |
| \(m\angle ABC=60^\circ\) |
I have been thinking about these two problems for some time, and I think I have finally cracked them! I'll now impart my knowledge to you!
1)
| \(\triangle ABC\text{ is an isosceles right triangle}\\ m\angle A=90^{\circ}\\ O\text{ is the circumcenter}\) | Given information |
| \(m\angle A+m\angle B+m\angle C=180^{\circ}\) | Triangle sum theorem (the sum of the interior angles of a triangle equals 180 degrees) |
| \(90^{\circ}+m\angle B+m\angle C=180^{\circ}\) | Substitution property of equality |
| \(m\angle B+m\angle C=90^\circ\) | Subtraction property of equality |
| \(m\angle B=m\angle C\) | Isosceles Triangle Theorem (The angles opposite congruent sides in an isosceles triangle are congruent) |
| \(m\angle B+m\angle B=90^\circ\) | Substitution property of equality |
| \(2m\angle B=90^\circ\) | Simplify |
| \(m\angle B=45^\circ\) | Division property of equality |
| \(\overline{AO}\cong\overline{BO}\) | Property of Circumcenter (The circumcenter is equidistant from the vertices of the triangle) |
| \(m\angle A=m\angle B\) | |
Well, this is taking some time...
Anyway, \(\triangle AOB\) is another isosceles triangle. \(m\angle OAB=m\angle B=45^\circ\), so the remaining angle, \(\angle BOA=90^\circ\)
.Hello DH,
Welcome to web2.0calc forum :))
Yes there are things you should know. ![]()
Our respected members are very polite and they use this site as a learning aid.
And they can also help others in this regard if they are reasonably sure that they know what they are talking about.
They do not use it for cheating on their assignments or getting their homework done for them.
They ask their question in a polite way using the word 'please' and then say 'thank you' when they are given an answer.
If they do not understand or they think the answer is wrong then they say so (with explanation) politely.
They also give answerer positive points if they are happy or even if they just want to recognise the effort the answerer has donated to them (sometimes even if they think the answer might be wrong). We do not encourage anyone to give negative points. You should have sound reason if you do this.
Respected members become known to us and they do tend to get priority treatment.
Reposts, if done properly also get priority treatment.
Here is info on reposting:
https://web2.0calc.com/questions/instructions-on-reposting_1