All Answers 357330 Answers

[7 + b]^6 - 7^6

b^6 + 42 b^5 + 735 b^4 + 6860 b^3 + 36015 b^2 + 100842 b + 117649 -7^6

Sub 8 for b

262,144 + 1,376,256 + 3,010,560 + 3,512,320 + 2,304,960 + 806,736

11,272,976 = 2^4 * 11 * 13^2 * 379

See WolframAlpha's various solutions here:

http://www.wolframalpha.com/input/?i=4%E2%88%9A15+-+10%E2%88%9A3%2F5%C2%A0%2B+3%E2%88%9A60

I don't believe yours is correct.... it would simplify to :  8√15

I guess the answer could be this:

10√15 - 2√15

Am I correct?

Manuel.... I made a typo on this question earlier....see my corrected answer here...

https://web2.0calc.com/questions/help-please_26975#r1

[ I verified my result with WolramAlpha...]

The answer is 13/20.

The easiest way is to write down all the possible totals eg 1from first spinner and 3 from the second gives a total of 4. There are 20 possible totals but some totals will occur more than once eg 7 occurs 3 ways ie 2,5 ; 3,4 and 4,3. Once you have all 20 it's then a matter of counting how many ways the totals of 5,6,7 and 8 occur.

sorry

Leonhard is doing a fundraiser for his school to buy AoPS books by running a lemonade stand. At the beginning of the day, Leonhard has 25 dollars of cash in his box. In the morning, he sells 8 dollars of lemonade, but he has to go to the grocery store and buy 5 dollars worth of sugar. At lunchtime, he sells 15 dollars worth of lemonade. In the evening, he has to go buy more lemons and the wind blows 3 dollars out of his box. The lemons cost 6 dollars. However, he also sells 25 dollars worth of lemonade during the evening. If Leonhard uses the money from his box to make his purchases, how much money should he have in his box at the end of the day?

He starts with $25.....to this he adds  $8 + $15 + $25   =  $73

From this....he subtracts  $5 + $3 + $6  = $14

So.....he should end up with  $73 - $14   =  $59

1- permutations{(2,3,4,5), 1}

{2} | {3} | {4} | {5} (total: 4)

2 -permutations{(2,3,4,5), 2}

{2, 3} | {2, 4} | {2, 5} | {3, 2} | {3, 4} | {3, 5} | {4, 2} | {4, 3} | {4, 5} | {5, 2} | {5, 3} | {5, 4} (total: 12)

3-permutations{(2,3,4,5), 3}

{2, 3, 4} | {2, 3, 5} | {2, 4, 3} | {2, 4, 5} | {2, 5, 3} | {2, 5, 4} | {3, 2, 4} | {3, 2, 5} | {3, 4, 2} | {3, 4, 5} | {3, 5, 2} | {3, 5, 4} | {4, 2, 3} | {4, 2, 5} | {4, 3, 2} | {4, 3, 5} | {4, 5, 2} | {4, 5, 3} | {5, 2, 3} | {5, 2, 4} | {5, 3, 2} | {5, 3, 4} | {5, 4, 2} | {5, 4, 3} (total: 24)

4-permutations{(2,3,4,5), 4}

{2, 3, 4, 5} | {2, 3, 5, 4} | {2, 4, 3, 5} | {2, 4, 5, 3} | {2, 5, 3, 4} | {2, 5, 4, 3} | {3, 2, 4, 5} | {3, 2, 5, 4} | {3, 4, 2, 5} | {3, 4, 5, 2} | {3, 5, 2, 4} | {3, 5, 4, 2} | {4, 2, 3, 5} | {4, 2, 5, 3} | {4, 3, 2, 5} | {4, 3, 5, 2} | {4, 5, 2, 3} | {4, 5, 3, 2} | {5, 2, 3, 4} | {5, 2, 4, 3} | {5, 3, 2, 4} | {5, 3, 4, 2} | {5, 4, 2, 3} | {5, 4, 3, 2} (total: 24)

Total =4 + 12 + 24 + 24 = 64 - permutations.

4.)

In triangle $ABC$, $m\angle A = 90^\circ$, $m\angle B = 75^\circ$, and $BC = \sqrt {3}$ units. What is the area of triangle $ABC$? Express your answer as a common fraction.

C

                 √3

A   90°           75°   B

sin 75°  =  AC / √3

AC  = √3* sin (75°)

Angle ACB  =  90 - 75  =  15°

sin(15°)  = AB / √3

AB  =  √3 * sin (15°)

So   the area  is

(1/2) AB * AC   =

(1/2) (√3 sin(15°) * √3 sin (75°)   =  (3/2)sin(15°)sin(75°)  =

(3/2)sin(15”) sin ( 90° - 15°)  =

(3/2)sin(15°)  (sin90”cos15°  - cos90°sin15°)  =

(3/2)sin(15°) (cos (15°) =        

(3/2)(1/2) sin (2 * 15)  =

(3/2)(1/2)sin(30°) = 

(3/2)(1/2)sin (30°)  =

(3/2) (1/2)(1/2)  =  3/8  units^2

4√15 - 10√3/5 + 3√60  =

4√15  - 2√3  +  3√[ 4 * 15]  =

4√15  - 2√3  + 3 [ √4  * √15 ]  =

4√15  - 2√3  + 3*2 *√15  =

4√15  - 2√3  + 6√15  =

10√15 - 2√3  

Edit to correct a typo

Angle AFB  =  Angle DFE

Angle DBA  = Angle FDE

Therefore, by AA congruency  Triangle DEF  is similar to Triangle BAF

But  DE  is  2/3  of DC.... and since AB  = DC, then  DE  is also 2/3 of AB

Then all  parts of triangle DEF  are 2/3  of  their corrresponding parts in triangle BAF

Thus....the altitude of triangle  DEF  is 2/3  of the altitude of triangle BAF

But the altitude of triangle DEF  = CG since they are parallel

And for the same reason, the altitude of triangle BAF   = BG

Thus  CG   =  2/3  of BG.....so ...  there are 5 parts of BC......and BG  is 3 of these

So  BG  =  3/5   of BC

And triangle BGF  is similar to  triangle BCD

But  BG  =  3/5  of BC....so  GF  =  3/5 of CD

So    GF  = FG  =   (3/5)  20    =   12

Thanks X!!

1 dgit numbers  = 4

2 digit numbers  = take any 2 of 4 numbers and permute them  =  P(4,2)  = 12

3 digit numbers  =   take any 3 of  4 numbers and permute them = P(4,3)   = 24

4 digit numbers  = permute all 4 numbers =  4!  =  24

So.....

4  + 12  +  2(24)    =     64 numbers 

We know that sec(x) is equal to cos(x) because it is the reciprocal of cosine.

So, choice d cannot be correct because cos(x) cannot be 0, because it would result in an undefined answer. 

We we know that cosine is adjacent/ hypotenuse. Of course, the reciprocal would be hypotenuse/adjacent. 

If if you look at choice b, c, and e, the numerators (hypotenuse) are all smaller than the denominator (adjacent side). This is not possible because the hypotenuse in a triangle cannot be less than one side. 

this is why choice A must be correct

I think I can answer #1

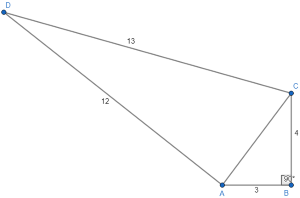
The diagram below meets all the given criteria. It is a quadrilateral with the given side lengths. Since $\overline{AC}$ is the hypotenuse of $\triangle ABC$, we can use the Pythagorean Theorem to find the length of the missing side length. Of course, this triangle satisfies the most famous pythagorean triple, a 3-4-5 right triangle, so $AC=5$.

Yet again, $\triangle DAC$ is in a similar situation. It is a 5-12-13 triangle, which is another Pythagorean triple. Because of this, $m\angle DAC=90^\circ$. 

I can break up the area of the original quadrilateral into two smaller parts: the 3-4-5 right triangle and the 5-12-13 right triangle. 

Using the formula $A_{\triangle}=\frac{1}{2}bh$, one can identify the areas of both triangles. This process is even simpler since the height of both triangles is also the perpendicular height. 

Now, just add the areas together. 

$A_1+A_2=A_{\text{total}}\\ 6+30=36\text{units}^2$

Many of the questions seem to suggest that there is a complementary diagram or some missing information (2, 3, 5 and 6)

We know that 23pi/2 is in between 270°(3pi/2) and 360°(2pi).

So, it's reference angle is 24pi/12 - 23pi/2 (because 2pi/1 is equal to 24pi/12).

The reference angle will be pi/12.

We know that sin+cos is equal to 90. and 90° in radians is pi/2. So, (pi/2) - (pi/12) will give you the value of theta, which is 5pi/12

In order to add these radicals, the radicals must be placed in simplest radical form. When a radical is in this form, the radicand (the number or expression contained inside the radical) must not have any perfect square factors, excluding 1. This process changes the way the radical looks, but it does not actually change the value.

Putting the radicals in simplest form requires one to identify a perfect square factor of the radicand. Let's try the first radical, $2\sqrt{18}$. In this case, the radicand is 18. A perfect square factor of 18 is 9 since 9*2=18. Let's break up the radicand in this fashion. 

$2\sqrt{18}\Rightarrow 2\sqrt{9*2}$

It is probably obviousn that both expressions are equivalent in value. Because a multiplication operation is being performed inside the radical and the multiplicand and multiplier are both positive, it is possible to split up the radical into two separate parts.

$2\sqrt{9*2}\Rightarrow 2\sqrt{9}*\sqrt{2}$

This manipulation of the original term has now created two radicals: $\sqrt{9}\text{ and }\sqrt{2}$. Notice that $\sqrt{9}$ can be simplified into something rational. In other words, $\sqrt{9}=3$. We can use this to simplify the radical even further.

$2\textcolor{red}{\sqrt{9}}*\sqrt{2}=2*\textcolor{red}{3}*\sqrt{2}=6\sqrt{2}$ 

Notice that the square root of 2 remains. The radicand, 2, has no perfect square factors, other than 1. I explained in the beginning that this indicates that a particular radical is in simplest form. In fact, we can use this exact process to simplify $\sqrt{32}$. I will use the same process, but I will skip the explanation portion.

$\sqrt{32}=\sqrt{4*8}=\sqrt{4}\sqrt{8}=2\sqrt{8}$

Actually, I need to explain something else for you! Ideally, you want to identify the LARGEST perfect square factor. In the preceding work I showed, I identified that 4 is a perfect square factor of the radicand, 32. This is true, but 4 is not the largest perfect square factor. If you keep searching, you will quickly realize that 16 is the LARGEST perfect square factor of 32. 

$\sqrt{32}=\sqrt{16*2}=\sqrt{16}\sqrt{2}=4\sqrt{2}$

Now,$\sqrt{32}$ is in simplest radical form. Sometimes, though, identifying the LARGEST perfect square factor may be impractical--especially if you are dealing with enormous numbers. Let's go back to the original approach I showed:

$\sqrt{32}=\sqrt{4*8}=\sqrt{4}\sqrt{8}=2\sqrt{8}$

Now, the radicand is 8. It, too, has a perfect square factor, which is 4. This means you can simplify further. 

$2\sqrt{8}=2*\sqrt{4*2}=2\sqrt{4}*\sqrt{2}=2*2\sqrt{2}=4\sqrt{2}$

Look at that! We arrived at the same answer as we did before. Therefore, always be sure that the resulting radical does not have any perfect square factors. Let's get back to the original problem. 

$2\sqrt{18}+\sqrt{32}\\ 6\sqrt{2}+4\sqrt{2}$

The whole point of putting both radicals into simplest form is that now they have identical radicals. We can now them together. 

$6\sqrt{2}+4\sqrt{2}=10\sqrt{2}$

I know that this is a long-winded explanation for such a simple problem. If you are confused, just ask away! I'll be glad to answer.

Another approach here without resorting to Trig is to just use similar triangles.

We have that

BC / CA   =   EF / FA

x / 28  =  5 / 7        multiplt both sides by 28

x  =  (28/7) *  5   =   4 * 5   =    20  ft

yea thanks

Good job, ACG......!!!....these Geometry problems are tough, sometimes...!!!

Manuel....I guess we have this :

³√ 5   ³√ 4

But......I'm not sure what you want to do with these.....we can't add them because we don't have the same quantities under the radicand

Multiplying them we get

³√20

I'm confused....!!!

The problem says that   y  =  8x + 17  .

To find  y  when  x = 0  ,  plug in  0  for  x  and solve for  y .

When  x = 0 ,   y  =  8(0) + 17   =   0 + 17   =   17

When  x = 1 ,   y  =  8(1) + 17   =   8 + 17   =   25

When  x = 2 ,   y  =  8(2) + 17   =  16 + 17  =   33

When  x = 3 ,   y  =  8(3) + 17   =  ...can you finish this?

And this is how to fill in the table...

Can you finish the last two?

Reason

1.   Given

2.   Vertical angles are congruent

3.   AA Similarity Theorem

Tan(A) = 5/7 =0.714......

5/7 = Height of tree / 28

Height of tree =5/7 x 28 = 20 feet.

Both triangles have a 90° angle. In order for the triangles to be similar, the sides that form this angle must be proportional, by the SAS Similarity Theorem.

If  △PRQ ~ △MRN , then  PR / RQ  =  MR / RN

Is it true that   PR / RQ  =  MR / RN   ?

PR / RQ  $\stackrel{?}{=}$  MR / RN

                                       Plug in the lengths of PR, RQ, MR, and RN.

12 / 18  $\stackrel{?}{=}$  8 / 6

                                      Reduce  12/18  by  3 .

4 / 6   $\stackrel{?}{=}$   8 / 6

4 / 6   ≠   8 / 6

Therefore  △PRQ  is not similar to   △MRN