All Answers 356331 Answers

Second one :

y  =  rx + s

       _____

        2x + t

Vertical asymptote  ⇒    x  = 3

2(3) + t  = 0

6 + t   = 0

t  =  -6

Horizontal asymptote ⇒  y  = -4

So     r/2 =  - 4  ⇒   r  = -8

And if  (1,0)  is the x intercept....we have that

-8(1) + s  =  0

s  = 8

And the function is  :

y  =    -8x + 8

         ________

          2x - 6

Here's the graph : https://www.desmos.com/calculator/bqxafolfmx

 ax + b

_____

  x + c

If the vertical asymptote is at x = 3 then c  = -3

If the horizontal asymptote is at   y   = - 4, then a  =  -4

If (1,0)  is an x intercept then we can solve this for b

-4(1) + b  = 0

b  = 4

So.....the function is

y  =  -4x + 4

       ______

          x - 3

Here's the graph  :  https://www.desmos.com/calculator/t5wbj4l2ad

log 15  =  x

And we can write

log₁₀ 15  = x

So....in exponential form, we have

10^x  = 15

b = 10      x  = x     n  =  15

Here's the way I set it up, ACG :

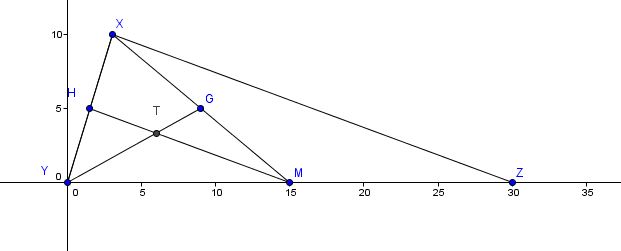
Look at  triangle YGM

Note that  G  is the midpoint of XM...so  the height of G  above base YM = the height of YGM  =  (1/2)height of triangle XYZ

And since M is the midpoint of YZ, it is  the base of YGM  =  1/2 base of triangle XYZ

And triangles are to each other as the ratio of their bases and heights

So area of triangle YGM  = (1/2)* (1/2 base of XYZ) * (1/2 height of XYZ) =

(1/4) (1/2 base of XYZ) *(height of XYZ)  

(1/4)area of XYZ  =   1/4 XYZ

Now  ...look at triangle YTM

Since YG is  a median of triangle YXM....then YT  = 2/3  of YG

But....this means that T  is (2/3)  the height above base YM that G is

So...the height of triangle YTM  =  2/3   height of triangle YGM

And they are on the same base 

So...the areas of triangles on the same base are to each other as their heights....so..

Area of triangle YTM  = (2/3)area of triangle YGM  =  (2/3)(1/4)XYZ  = (1/6)XYZ

So....area  of triangle  MTG  = 

Area of triangle YGM - Area of triangle YTM =

(1/4)XYZ - (1/6)XYZ  =

(1/4  - 1/6) XYZ =

(2/24)XYZ  =

(1/12)XYZ =

(1/12)(150)  =

12.5 units^2 

log₅ 36 = x

Exponential form  :       5^x  = 36

b  =  5       x = x      n = 36

5.

y =  5/x      4 to the left....3  up   =

y  =  5 / (x + 4)  +  3     first answer

6.....the points of discontinuity  can be found by factoring the denominator 

x^2  + 4x  -  5  

(x + 5) (x - 1)

Setting each factor to 0  and so;ving for  x

x + 5  = 0                x - 1  = 0

x  = -5                      x  = 1        these are the discontinuities

7

   x - 5                         x - 5

__________   =       _________

x^2 +4x + 3              (x + 1) ( x + 3)

We can see that we will have discontinuities (asymptotes) at  x  = -1  and x  = -3

There will be no holes because no factors "cancel" 

t^2  + 4t - 12

__________

t^2  - 4

(t + 6)(t - 2)

_________

(t + 2) ( t - 2)

  (t + 6)

______

   (t + 2)     and   t cannot be  -2  or + 2

Thank you!!

Need help

2⁵  = x

log₂ x  = 5

b = 2    x  = 5    n  = x

2x      -     x+ 7

___         ____

x - 7          x

(2x)x  -  (x + 7) (x - 7)

_________________

       x (x - 7)

2x^2  - [ x ^2  - 49 ]

_______________

    x ( x - 7)

2x^2  - x^2   +   49

_______________

    x ( x - 7)

x^2  + 49

________

 x  ( x - 7)     

Ahhhhh, thank you both of you so much!!! <3

We can use the arctangent here

arctan (3/4)  = C ≈  36.87°

Second one..we know the opposite side to R and the hypotenuse...so....we can use the arcsin

arcsin (30/40)  = R ≈ 48.59°

Angle c is arcsin (3/5)    (remember sin is  opp/hyp)   = 36.87 degrees

Similar here   angle r     =  arcsin (30/40) = 48.59 degrees

(n - 3) / (n^2 + 6n + 8)

_________________

        (n + 1)

        _____

        (n + 2)

    ( n - 3)                          ( n + 2 )

___________    *            ________

n^2 + 6n + 8                     ( n + 1)

(n - 3) (n + 2)

__________________

(n + 4) ( n + 2) (n + 1)

(n - 3 ) ( n + 2)

____________

(n + 4) ( n + 1)

thanks cphill

d^2 - 9d + 20           d^2  -2d - 8 

___________  +    ______________

d^2  - 3d - 10          d^2  +4d  - 32

(d -5) ( d - 4)    +    (d -4) (d + 2)

___________         ___________

(d - 5) ( d + 2)        (d + 8) ( d - 4)

(d - 4)       +    (d + 2)

_____            _____

(d + 2)            (d + 8)

(d - 4)(d + 8)  +  (d + 2) (d + 2)

________________________

      (d + 2)  (d + 8)

d^2 - 4d + 8d - 32  + d^2 + 2d + 2d + 4

_______________________________

   (d + 2) (d + 8)

2d^2  + 8d - 28

_____________

(d + 2) (d + 8)

Very nice, Omi   !!!!

Horizontal  asymptote  =  y  = -4/8  =   -1/2

See my answer here :

https://web2.0calc.com/questions/need-some-help_11

We have the following relationship :

MN  ( MN + NO)   = MP ( MP +  PQ)    which means that

MN ( MN + NO)  =   MP(MQ)

NO  =  6

MN  = 3

MQ  = 15

So 

3 (3 + 6)  = MP (15)  

3 (18)  =  15 * MP   

54  =  15 * MP      divide both sides by  15

54/15  = MP   =  18/5

2.  In  an inverse relationship......the number of people  * cost per person = total cost is constant

So....the total cost  is

44 * 30   =  $1320

So.....to find the cost per person if 20 pepole go we have that

20 *  cost per person  =  1320        divide both sides by 20

cost per person  =  1320 / 20   =  $66

Area of sector  =  (1/2)r^2 * (theta in rads )

So

15.3  = (1/2) (3)^2 *  ( theta in rads)

15.3   =  9/2   * (theta in rads )       multiply both sides  by  2/9

15.3 (2/9)  =  (theta in rads)

3.4   =   theta  in rads

To  conert this to degrees  we have

3.4    *  180° / pi   ≈  194.8°

To  find the arc length, S,     we have

S    =  2 * pi  (radius)   (194.8 / 360)  =

2 * pi * 3  *  (194.8 / 360)  =  

6* ( 194. 8 / 360)  * pi   ≈   81.26 m

To convert the exponential form   b^x   = n      to log form   we have

log_b n  =  x

So

10^x  =  25    becomes

log₁₀ 25  =  x

So    b  =  10      x =  x        and    n  =  25   

Hope that's not too confusing !!!