All Answers 356353 Answers

Arithmetic sequence with d = 18

26 + 44 + 62 + 80 + 98 + 116 + 134  =        ad 'em up to see what you get !

Or use     SUM =  n ( a1+a7)/2  =    7 (26+134)/2 = ??

4.)  d = 5  so 5n is good..... first one starts with 54 ...no good    second choice only has 13 terms...no good

           third choice  starts with 49 and has 5n and has 14 terms.....goood!     Fourth choice has 44 terms....no good

5.

n =1         = 5

    2           =6

    3             7

    4             8         Add 5   6  7   8   and you get ? 

(2 + 2i)^8  =

r  = √ [ 2^2 + 2^2 ]  =  2√2

tan  θ  =  2/2   =  1 

 θ  = pi/4

(2 + 2i)^8  =  (2√2)^8* e^(i * 8pi /4 )  =   (2√2)^8 *e^( i * 2pi)  =

4096 ( cos 2pi + i * sin (2pi) )  =

4096 ( 1 + 0i )  =

4096

Lesson 12: Voices of Modernism (1920s–1940s) Unit Test 

you probably wouldn't know it.

#37. Many of the stories in this unit have a theme of loss common. Which story evokes the most pathos?

yeah with english class i need help

I will take a crack at it !!

Let the total amount they started with = m

m / [7+6+5] + 12 = m / [6+5+4]

m =$1,080 - the amount of money they started with as follows:

1,080 / 18 = 60 - average share of each, but we have a ratio of 7:6:5, so:

$420:$360:$300

1,080 / 15 = 72 - the average share of each AFTER the game!!, but we have 6:5:4, and:

72 / 6 = $12 - this is winning of the gambler who started with:

$420 and ended up winning $12, since the ratios are in the same order, so they ended up with:

$12, $10, $8 =$30 in total winning !!!!

Note: Somebody should check these crazy numbers!! But then, I don't gamble!!!!.

the hamburger i can answer. 

Grill it until its not pink on the inside and until it is nice and greasy. If you don´t like greasy hamburgers then push it down with the spatula twice every flip

thank gosh you came. ive been stuck on this for two days!

2000 x 5% = 2000 x .05 = $100   PLUS

5740 x 8% = 5740 x .08 =  459.20    

total commission = 100 + 459.2 = $559.20

Here's the image. If you want to print it or draw on it, you can.

The equation of the first circle is \((x+3)^2+(y)^2=64\) (red) and the second is \((x+3)^2+(y+2)^2=256\) (blue).

Equations 1 and 4 are correct I think, since a dilation of 2 multiplies the radius of 8 to 16 and all circles are similar.

Solve for i:

A = P (i + 1)

A = (i + 1) P is equivalent to (i + 1) P = A:

P (i + 1) = A

Divide both sides by P:

i + 1 = A/P

Subtract 1 from both sides:

i = (A - P) / P     OR       i=A/P - P/P=A/P - 1. Yes, the two are equivalent!! The reason is very clear if you look at the last one.

\(\displaystyle x^{2}+y^{2}+z^{2}=49,\)

is the equation of a sphere radius 7, centered at the origin, so what you are looking for are points on its surface such that all three co-ordinates are integers.

I don't see any way through it other than by trying each integer value of one of the variables in turn.

Choosing z, it's largest value is 7, and that gets us 

\(\displaystyle x^{2}+y^{2}=0, \text{ from which we have } x=0\text{ and }y=0.\)

If z = 6,

\(\displaystyle x^{2}+y^{2}=13,\text{ leading to }x=\pm2, y=\pm3,\text{ or }x=\pm3,y=\pm2.\)

If z = 5,

\(\displaystyle x^{2}+y^{2}=24,\text{ and there are no integer solutions for that.}\)

So on through to z = -7.

A customer ordered 15 pieces of gourmet chocolate.
The order can be packaged in small boxes that contain 1, 2 or 4 pieces of chocolate.
Any box that is used must be full.
How many different combinations of boxes can be used for the customer's 15 chocolate pieces?
One such combination to be included is to use seven 2-piece boxes and one 1-piece box.

\( \small{\text{In $15$ pieces max. $\color{red}3$ ($\color{green}4$-piece boxes), max. $\color{red}7$ ($\color{green}2$-piece boxes), and max. $\color{red}15$ ($\color{green}1$-piece boxes) }} \\\\ \)

\(\small{ \begin{array}{|rcll|} \hline && \displaystyle \left(\sum\limits_{i=0}^{\color{red}3} x^{({\color{green}{4}}*i)} \right) \times \left(\sum\limits_{i=0}^{\color{red}7} x^{({\color{green}{2}}*i)} \right) \times \left(\sum\limits_{i=0}^{\color{red}15} x^{({\color{green}{1}}*i)} \right) \\\\ &=&(1+x^4+x^8+x^{12}) \times (1+x^2+x^4+x^6+x^8+x^{10}+x^{12}+x^{14}) \times \\ && \times (1+x^1+x^2+x^3+x^4+x^5+x^6+x^7+x^8+x^9+x^{10}+x^{11}+x^{12}+x^{13}+x^{14}+x^{15} ) \\\\ &=& x^{41} + x^{40} + 2 x^{39} + 2 x^{38} + 4 x^{37} + 4 x^{36} + 6 x^{35} + 6 x^{34} + 9 x^{33} + 9 x^{32} + 12 x^{31} + 12 x^{30} \\ &+& 16 x^{29} + 16 x^{28} + 20 x^{27} + 20 x^{26} + 22 x^{25} + 22 x^{24} + 24 x^{23} + 24 x^{22} + 24 x^{21} \\ &+& 24 x^{20} + 24 x^{19} + 24 x^{18} + 22 x^{17} + 22 x^{16} + {\color{red}20 x^{15}} + 20 x^{14} + 16 x^{13} + 16 x^{12} \\ &+& 12 x^{11} + 12 x^{10} + 9 x^9 + 9 x^8 + 6 x^7 + 6 x^6 + 4 x^5 + 4 x^4 + 2 x^3 + 2 x^2 + x + 1 \\ \hline \end{array} } \)

\(\text{The coefficient from $\small{ \color[rgb]{1,0,0}{x^{15}} } $ is $\small{ \color[rgb]{1,0,0}{ 20 } } $. } \\ \text{So there are $\mathbf{20}$ possibilities.} \)

\(\begin{array}{|r|r|r|r|} \hline & \color{green}{1}\text{-piece boxes} & \color{green}{2}\text{-piece boxes} & \color{green}{4}\text{-piece boxes} \\ \hline 1 & 15 & & \\ \hline 2 & 13 & 1 & \\ \hline 3 & 11 & 2 & \\ \hline 4 & 11 & & 1 \\ \hline 5 & 9 & 1 & 1 \\ \hline 6 & 9 & 3 & \\ \hline 7 & 7 & & 2 \\ \hline 8 & 7 & 2 & 1 \\ \hline 9 & 7 & 4 & \\ \hline 10 & 5 & 1 & 2 \\ \hline 11 & 5 & 3 & 1 \\ \hline 12 & 5 & 5 & \\ \hline 13 & 3 & & 3 \\ \hline 14 & 3 & 2 & 2 \\ \hline 15 & 3 & 4 & 1 \\ \hline 16 & 3 & 6 & \\ \hline 17 & 1 & 1 & 3 \\ \hline 18 & 1 & 3 & 2 \\ \hline 19 & 1 & 5 & 1 \\ \hline 20 & 1 & 7 & \\ \hline \end{array}\)

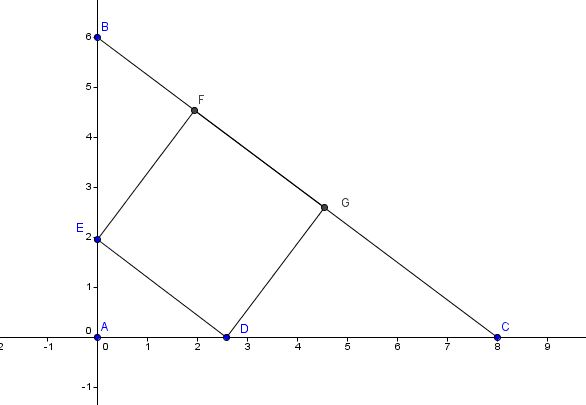
Let two vertexes of the square lie on  (a,0) and (0, b)

Where a < 8    and b < 6

Let side BC be the hypotenuse of the right triangle

And the equation of BC is:

y  =  -(6/8)(x - 8)

8y = -6x + 48

6x + 8y - 48 = 0

Now....using the formula for the distance between a point and a line we have two outcomes

Distance between (a,0)  and the line  =

abs [6(a) + 8(0) - 48 ]           abs[    6a  -  48]          abs[ 3a  - 24]

_________________      =    ____________      =   _________

     10                                        10                                    5

Distance between (0,b) and the line =

 abs[6(0) + 8(b -48) ]         abs[  8b - 48]              abs [ 4b - 24]

 ________________      =  ___________    =      ___________

     10                                       10                                5

And these distances are equal

Since a < 8  and b < 6 we can write

(24 - 3a) / 5  = (24 - 4b) / 5

24 - 3a  = 24 - 4b

-3a  = - 4b

3a = 4b  ⇒  b = (3/4) a

And the distance between the two points = the distance from one of the points to the hypotenuse 

Thus...

√[a^2 + b^2]  =  abs (3a - 24 )/ 5

Since  a < 8,  and the left side must be > 0...we can write...

√[a^2 + b^2]  =   (24 - 3a ) / 5

√ [a^2 + (9/16)a^2 ]  =  (24 - 3a) / 5

√ [ 25a^2] / 4  =  (24 - 3a)/5

5a/4  =  (24 - 3a) / 5

25a/4 = 24 - 3a

25a  = 96 - 12a

37a = 96

a = 96/37     

b =  (3/4 a)   = (3/4)(96/37) =   72/37

So.....the length of the side of the square  =

√[(96/37)^2 + (72/37)  ^2]  =

√[96^2 + 72^2] / 37   =  √14400 /  37    =   120 / 37 cm 

Here's a pic.... D  = "a"  = (96/37, 0)   and  E = "b"  = (0, 72/37)

Numbers beginning with 2 =2C2 =1

.......................................3 =3C2 =3

.......................................4 =4C2 =6

.......................................5 =5C2 =10

,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,6 =6C2 =15

.......................................7 =7C2 =21

.......................................8 =8C2 =28

.......................................9 =9C2 =36

There are a total of = 120 descending numbers

We have 5 equal segments on EF ...and we are looking for the point that is 3/5 of the way between E and F in that directon

So we have

( -1 + (3 - (-1) )(3/5) , 6 + (9 - 6)(3/5) )  =

(-1 + (4)(3/5) , 6 + (3)(3/5) )  =

(-1 + 12/5 , 6 + 9/5 )

(7/5, 39/5)

We have  4 equal divisions.....so we are looking for the point that is 1/4 the distance between AB in that direction...so we have...

( 4  + [ 12 - 4] (1/4), 9 + [ -5 - 9] (1/4) )   =

( 4 +  (8)(1/4), 9 + (-14)(1/4) )  =

( 4 + 2,  9 - 14/4 )  -

(6,  9 - 7/2 )

(6, 11/ 2 )

The answer is 24.

The answer is 24.