All Answers 358184 Answers

\(N_{left} = N_{girl}\cdot P[\text{girls are left handed}]+N_{boy}\cdot P[\text{boys are left handed}]\\ N_{left} = 320 \cdot 0.2 + 250 \cdot 0.1\\ N_{left} = 64+25 = 89\)

No prob, Jenny.....!!!

Oh yes! I remember this now I went over it in my lesson Thank you! I apprecitate it.

This is kind of counter-intuitive....but......

The  "1/4"   means that we have a horzontal stretch of the original  function  by a factor of 4.....  [ the reciprocal of the fraction ]

In general  we have   y = log (b x)

When b > 0 but  < 1.....we have  a horizontal stretch of y = log (x)

When b > 1......we have a horizontal "compression"   of y = log(x)....   [ not, "comprehension" ]

So... y = log (4x)    has a compression  and  the compression  factor is a reciprocal of 4  =  1/4

Look at the graphs, here : https://www.desmos.com/calculator/tbguagxjhp

Remember that  a^m  x a ^n   =  a^(m + n)

So.....the numerator becomes

3^8  x 3^4   = 3^(8 +4)  =  3^12

And the denominator becomes

3^ 2  x 3^8  =  3^(2 + 8)  =  3^(10)

So  we have

3^12

_____        (1)

3^10

And

a^m

____    =     a^(m - n)

a^n

So (1)  evaluates to    3^(12- 10)   =  3^2  

We have the following "formula"

A  = P ( 1 + r)^t

Where

A = 800

P = 500

r = 1.5%  = .015

And we are looking for t

So we have

800  = 500 ( 1 + .015)^t       divide both sides by 500

(800/500)   =  (1 + .015)^t

(8/5) = (1.015)^t        take the log of both sides

log (8/5)  =log (1.015)^t        and we can write

log(8/5)  = t * log (1.015)     divide both sides by  log(1.015)

log(8/5) /log (1.015)  = t ≈  31. 57  yrs  =  32 years (to the nearest year)

Thanks, hashtagmath.......

 Your answers are well-presented......!!!

Answered here :   https://web2.0calc.com/questions/geometry-problem_21#r1

There may be a much easier way to do this, but we can find the volume of the frustum by creating a cross-sectional kite .......the sphere will  have a circular cross-section and the frustum will have a cross-sectional trapezoid 

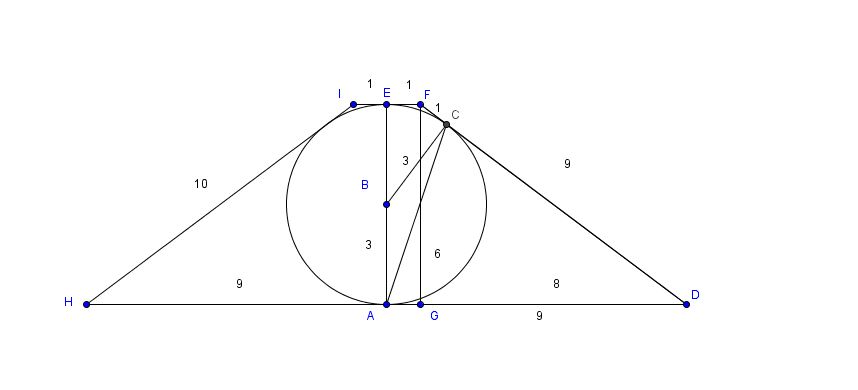
First......since the sphere is tangent to the frustum at both the top and bottom bases, the frustum height  is  =  6

So.....we can create a 6-8-10  Pythagorean right triangle DGF  as shown in the illustration - with one leg of 6 - (GF)  - one leg of 8 - (DG) -  and the slant height - (DF)  -forming the hypotenuse........the cosine of  angle FDG  ( at the bottom right vertex of the frustum ) =   8/10   =  4/5

Now......the radii of the circle will form kite  ABCD  

Connect AC......angle ABC will be supplementary to angle FDG......so its cosine  = -4/5

And because DA and DC are tangents drawn from the same point D, they are equal

And we can use the Law of Cosines to find AC

Note: AB  and BC are radii of the circle

AC^2 =  AB^2 + BC^2  - 2(AB)(BC)(cos ABC)

AC^2  =  3^2 + 3^2  - 2(3)(3) (-4/5)

AC^2 = 18  + 72/5

AC^2  =  [ 90 + 72] / 5

AC^2  =  [ 162 / 5 ]

And Using the Law of Cosines once more, we can find the lenths of DA and DC.....let their lengths = x......and we have

AC^2  =   x^2 + x^2  -  2 (x^2)cos(CDA)

[ 162 / 5 ]  =  2x^2 - 2x^2 [ 4/5 ]

[162/ 5 ]  = 2x^2 [ 1 - 4/5]

[ 162 / 5 ] = 2x^2 [ 1/5]

162 = 2x^2

x^2  = 81

x = 9  =   DA  =  DC

But DA  =  radius  of the bottom base of the frustum

And since DC = 9.....then CF  = FD - DC  =  10 - 9   =  1

But CF = FE since they are tangents drawn from the point F

And FE  =  radius of the top base of the frustum

So.....using the fomula for the volume of a frustum, we have

V  = pi * GF * ( DA^2 + DA*FE^2 + FE^2 ) / 3  

Where 

GF  = frustum height

DA =  radius of bottom base

FE = radius of top base

So we have

pi * ( 6) *  ( 9^2  + 9 * 1 + 1^2 ) / 3  =

pi (6)  ( 81 + 9 + 1 ) / 3    =

pi (6) (91) / 3  =

2  * 91 pi  =

182 pi  units^3

1. standard form of a linear equation, like yours is  \(ax^2+by = c\). So it would be written as \(8x-10y = 7\).

2. The y-intercept of a graph is when the x-value is 0. So in this equation, we can set x to 0. \(3(0) -5y = 7 \implies -5y = 7 \implies y = -\frac{7}{5}\)

3. We know we find the equation with point-slope form, which is \(y-y_1=m\left(x-x_1\right)\) where m is the slope. \(y_1\) is the y-value of any of the points. and \(x_1\) is the value of the x-coordinate corresponding with the y-coordinate. So we can simplify to \(y-3=m\left(x-3\right)\)Then we can find the slope of the graph from the two points. which is 2/5. Then we plug in the values and solve\(y-3=m\left(x-3\right) \implies y-3=\frac{2}{5}\left(x-3\right) \implies y - 3 = \frac{2}{5}x - \frac{6}{5} \)\(\boxed{y = \frac{2}{5}x + \frac{9}{5}}\)

4. We can begin by putting line 1 in slope intercept form. 8y = -5x -9. y = -5/8x - 9/8. If line 2 is going to be perpindicular to line 1, their slopes are going to be opposite reciprocals of each other. So the slope of line 2 is 8/5. Then like in problem 3, we can use the point slope form. \(y-y_1=m\left(x-x_1\right) \implies y-y_1=\frac{8}{5}\left(x-x_1\right)\) We also have the point (10,10). So we can substitute the point in the equation. \(y-y_1=\frac{8}{5}\left(x-x_1\right) \implies y-10=\frac{8}{5}\left(x-10\right) \implies y -10 = \frac{8}{5}x - 16 \implies y = \frac{8}{5}x -6\)8/5 is m, and -6 is b. 8/5 + (-6) = 8/5 - 6  = \(\boxed{-\frac{22}{5}}\)

5. We can start by finding the equation of the line segment using the point-slope form. \(y-y_1=m\left(x-x_1\right) \implies y-2=m\left(x-1\right)\)We can find the slope from the points and see it is 1/3. So \( y-2=\frac{1}{3}\left(x-1\right) \implies y - 2 = \frac{1}{3}x - \frac{1}{3} \implies y = \frac{1}{3}x + \frac{5}{3}\) Then we know that the perpindicular bisector has an opposite reciprocal slope. So \(\boxed{y = -3x + \frac{5}{3}}\)is the equation of the perpendicular bisector. 

Hope that helps!

each one has a chance of 1/12,so if you do it 13 times,it is 12 times 13,which is 132. However,that is only for one side. You have to multiply that by the number of sides on a rubix cube,plus the factors of the table and the location of the spin. However,this is all easier said than done. If someone else could calculate these factors,that would be the correct answer.

Six sides of the cube can be rotated two ways so 12 possible moves each time....(?)

  each move has only 1/12 of a chance of being the same

I think this is going to be a very large denominator fraction!..

Wait a minute....I think you can move the MIDDLE  of a face.....right?

    SO the number of moves would be even larger (depending on the size of the cube)

       Mind numbing  trying to visualize.   I think a 3 x 3 has 18 possible moves each time....

I played prodigy tbh.

...the only other one left     CSYT eliminated 12.5 and t......soooooo....... ?

 1

 4 8 16 32 64 128

 9 27 81

 25 125

 36

 49

 100

 121

 144
17 out of 150 ARE perfect powers

so   133/150   

Corrected....thanx guest

Thank you which is the independent?

Thanks!

12.5 is definitely not a variable, as it cannot change its value. Therefore, we can easily eliminate 12.5

Now, let's see. Does \(g\) "depend" on \(t\) or is it the other way around?

Or, look at it this way. The definition of a dependent variable is the variable that is evaluated. We are not looking for \(12.5g\), instead, we are looking for \(t\) .

Therefore, \(t\) is the dependent variable.

You are very welcome!

:P

You can use the constant acceleration equation: v = u + a*t  where u = initial vertical velocity = 2.37*sin(56.6°) m/s here; v = final vertical velocity = -u (when she hits  the ground again); a = -9.8m/s² (acceleration due to gravity); t = time in the air:

 -2.37*sin(56.6°) = 2.37*sin(56.6°) - 9.8*t

t = 2*2.37*sin(56.6°)/9.8 s   

Bekah has four brass house number digits:
2, 3, 5 and 7, and only has one of each number.
How many distinct numbers can she form using one or more of the digits?

\(\text{binary code} \\ \begin{array}{|c|c|c|c|r|c|} \hline 2 & 3 & 5 & 7 & & \text{distinct numbers} \\ \hline 0&0&0&1 & 7 & 1! \\ 0&0&1&0 & 5 & 1! \\ 0&0&1&1 & 57 \text{ or } 75 & 2! \\ 0&1&0&0 & 3 & 1! \\ 0&1&0&1 & 37 \text{ or } 73 & 2! \\ 0&1&1&0 & 35 \text{ or } 53 & 2! \\ 0&1&1&1 & 357 & 3! \\ 1&0&0&0 & 2 & 1! \\ 1&0&0&1 & 27 \text{ or } 72 & 2! \\ 1&0&1&0 & 25 \text{ or } 52 & 2! \\ 1&0&1&1 & 257 & 3! \\ 1&1&0&0 & 23 \text{ or } 32 & 2! \\ 1&1&0&1 & 237 & 3! \\ 1&1&1&0 & 235 & 3! \\ 1&1&1&1 & 2357 & 4! \\ \hline &&&&\text{sum}& = 4\times 1! + 6\times 2! + 4\times 3!+1\times 4! \\ &&&&& = \dbinom{4}{1}1! +\dbinom{4}{2}2! +\dbinom{4}{3}3! +\dbinom{4}{4}4! \\ &&&&& = 1!C_4^1 +2!C_4^2 + 3!C_4^3 + 4!C_4^4 \\ &&&&& = 4+12+24+24 \\ &&&&&\mathbf{ = 64} \\ \hline \end{array}\)

B

2

X

1

A     1     Y         2               C

Note that   BX  = 2AX

And  YC  =  2AY

So we have that

(3AX)^2 + AY^2  = BY^2   ⇒   9AX^2 + AY^2  = 256  ⇒  AY^2  = 256 - 9AX^2    (1)

And

AX^2  + (3AY)^2  = 28^2  ⇒  AX^2  + 9AY^2  = 784  (2)

Subbing (1)  into (2)  we have

AX^2 + 9(256 - 9AX^2)  = 784

AX^2 + 2304 - 81AX^2  = 784

-80AX^2  = -1520

AX^2  =  -152 / - 8

AX^2 = 19

AX = sqrt(19)

So....BA  =  3AX  =  3sqrt(19)

And

AX^2 + 9AY^2  = 784

19 + 9AY^2  = 784

9AY^2  = 765

AY^2 =  85

AY  =  sqrt (85)

So AC  = 3sqrt (85)

So  BC  =  sqrt  [ BA^2 + AC^2 ] = 

sqrt [ 9 * 19 + 9 * 85 ] =

sqrt [ 9 ( 19 + 85)  ]  =

3sqrt (104) =

3sqrt ( 26 * 4)  =

2 * 3 sqrt (26)  =

6 sqrt (26)