All Answers 357307 Answers

Hint, it will be easier to do if you divide every term by 2 to start with.

this is the question.

I'm not so sure about this Chris.  In statement: "Then by SAS , triangle ABE  is congruent to triangle CBE" you have assumed that the bisector of ABC meets the bisector of BCD at the same point on AD (and you then proceed to show everything is consistent if this is the case).  In other words, you have assumed what you set out to prove!  I think you should start with the assumption that the two bisectors meet at potentially different points, say E and F, on AD, and then show that E and F must be the same point.  

Should this be:

   ? - 3 = ?

-(6 -  2 = 4)

---------------

  ? -  1 = ?

If so, rewrite as:

  a - 3 = b

-(6 - 2 = 4)

--------------

  c - 1 = d

In this case there are an infinite number of solutions!

We have four equations:

a - 3 = b        

a - 6 = c      

c - 1 = d       

b - 4 = d     

These are satisfied by

a = 7 + p,   b = 4 + p,   c = 1 + p,   d = p  where p is any number

So for example, if p = 0, then a = 7, b = 4, c = 1 and d = 0

If p = 4, then a = 11, b = 8, c = 5 and d = 4

etc.

Hello Melody,

of course there is x = 8.

$8x + 1 \equiv 5 \pmod{12}\\ 8x \equiv 4 \pmod{12}\\ 8x = 12k + 4,~k \in \mathbb{Z}\\ 2x = 3k + 1,~k \in \mathbb{Z}\\ 2x \equiv 1 \pmod{3} \\ \text{now the tricky part}\\ 2^{-1} \pmod{3} = 2\\ x \equiv 2 \pmod{3}\\ \text{the problem states }a<2, \text{ this is an error, it should be }a\leq 2$

Thank you so much!

Sine wave for sure !!!  ⇒   "C"

Frequency =  1 / period  =   1 / 0.0038    =   263.16 Hz

Thanks, hectictar.....been missing you on here.......!!!!

A.  period

Thanks MediumRareRibeye....!!!!

Sounds like a good idea....!!!!!

I think this may prove it :

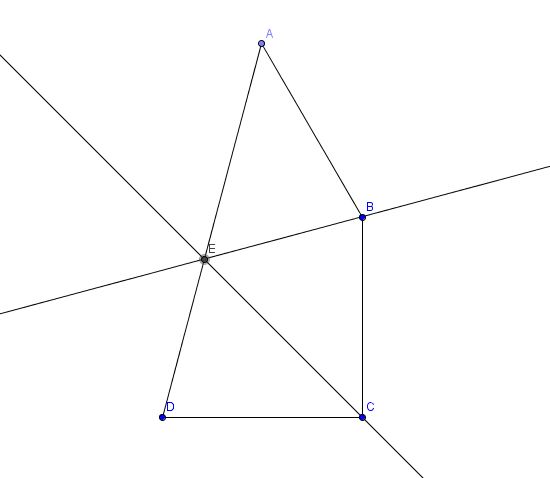
Let the sum of angles ABC and BCD = 240°

And let the bisectors of angles ABC and BCD  be as shown

Since AB = BC = CD

Then by SAS , triangle ABE  is congruent to triangle CBE

Similarly, by SAS, triangle CBE is congruent to triangle CDE

So....triangle CDE is congruent to triangle ABE is congruent to triangle CBE

So  angles DEC, AEB and BEC are congruent

But angles ABC and BCD sum to 240

So   1/2 ABC + 1/2 BCD = 120

But 1/2ABC = EBC

And 1/2 of BCD = BCE

So  angles EBC and BCE = 120

So angle BEC = 180 - (m EBC + BCE) = 180 - 120 = 60

But BEC = AEB = DEC.....so....

60 + 60 + 60  =  180

Therefore angle AED must be  straight a straight angle because  angle AEB + angle BEC + angle DEC  =  60 + 60 + 60  = 180

Thus....E must lie on AD.......and E is the intersection of the bisectors of angles ABC and BCD

Correction: If x,y are positive real integers such that x can be expressed as a continued fraction of $\frac{a}{\frac{b}{\frac{b}{\frac{b}{\cdots}+\frac{x}{\cdots}}+\frac{x}{\frac{b}{\cdots}+\frac{x}{\cdots}}}+\frac{b}{\frac{b}{\frac{b}{\cdots}+\frac{x}{\cdots}}+\frac{x}{\frac{b}{\cdots}+\frac{x}{\cdots}}}}$ and a is the least prime number which has the property that any sum of two nonnegative consecutive integers is divisible by it. B has the property that it is the first prime number which is not a factor of any other prime number, and it also does not equal to A. Y has the property that the sum of an infinite geometric sequence with a scale factor of 1/2 with starting term one is equal to y plus $e^{\pi i}$. What is x+y?

HAPPY  BDAY

you have helped me so much !!!!!

$\sqrt{25}=5\\ \frac{2\sqrt{25}}{4\sqrt{10}}=\frac{2*5}{4*\sqrt{10}}=\frac{5}{2\sqrt{10}}\\ \text{Multiply the numerator and denominator by the denominator to get rid of the radical on the bottom}\\ \frac{5}{2\sqrt{10}}*\frac{2\sqrt{10}}{2\sqrt{10}}\\ \frac{10\sqrt{10}}{4*10}=\frac{\sqrt{10}}{4}$

Thanks, ILP!!!!

I think there is some missing info here....