All Answers 358335 Answers

"with vertex"....????

Which vertex ???

Wow! Thanks so much! I finally get it now. This was a big help for me. Thanks especially for doing it so quickly! :)

P(2 + i) = 4 - 3i

and

Q(2 + i) = P(2 + i)

Which implies that

Q(2 + i) = 4 - 3i

And Q (x ) = ax+ b

So

Q ( 2 + i)  =  a (2 + i) + b  =   2a +ai + b  

And

2a + ai + b  =   4 - 3i

So.....this implies that

(2a + b) + ai   =   4 - 3i         equate co-efficients

2a + b = 4

a = - 3

So

2(-3) + b = 4

-6 + b = 4

b = 10

So

Q(x)  =  -3x + 10

Check

Q(2 + i)  =  -3(2 + i) + 10   =  -6 - 3i + 10  =  4 - 3i

Oh ok! Thanks so much for the clarifications Melody. 

And yes, I'll make sure to leave a good impression! :'D

Hi Noobie,

Welcome to the forum, I am pleased that you have made an account.   

The explanations pages are not likely to change anytime soon.  (it is a pity)

If you have specific queries you can ask on the forum. 

If you make a good impression here you will be well answered :)

Thank you, guys!

Note that we can rearrange this as

100^2 - 1^2  +  99^2 - 2^2  + 3^2 - 98^2 + 4^2 - 97^2 + .....

(100+ 1) (100 - 1) + ( 99 + 2) (99 - 2) + (3 + 98) (3 -  98) + (4 + 97)(4 - 97) +....

(101) (99 + 97 - 95 - 93.....)  =

(101) (99 - 95 + 97 -  93..... )   =

(101) ( 4 + 4.....)   

We paired 4 terms to get one 4

We paired 8 terms to get two 4's

So......pairing 100 terms will yield twenty-five 4's

So.....the sum is  (101)(25 * 4)  =  101 * 100 = 10100

That is correct Zeet.    

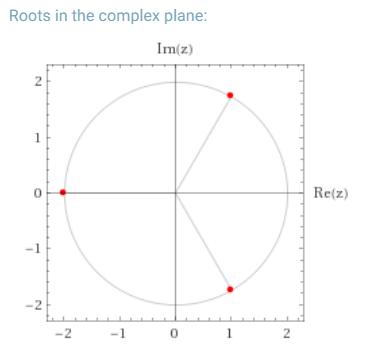
The only real solution is z=-2

but I think mathtoo wants the complex solutions too.  It is a cubic so there are 3 solutions altogether.

There will be equally spaced at   \(\frac{2\pi}{3}\)   radians apart on the complex plane. So the others are at \(\frac{\pi}{3}\;\;and \;\;\frac{-\pi}{3}\)

The modulus or absolute value is 2

so

\(z=-2,\;\;2e^{(\pi/3)i},\;\;2e^{(-\pi/3)i}\)

\(2e^{(\frac{\pi}{3})i}\\=2[cos(\pi/3)+isin(\pi/3)]\\ =2[\frac{1}{2}+i\frac{\sqrt3}{2}]\\ =1+i\sqrt3\\~\\ 2e^{(\frac{\pi}{3})i}\\ =1-i\sqrt3\)

so

\(z=-2,\;\;1+i\sqrt3,\;\;1-i\sqrt3\)

Here is the diagramatic representation.  Copied from Wolfram|Alpha.

Thanks Chris :)

LOL. You really got me with that pun there. Lmao

it should be + 5, but I got the right answer already.

thanks! :)

if the question is find z because im not sure,

z^3 = -8 

(-2)^3 = -8

therefore z = -2

Thank you, Rom! 

This is also distinguishability with duplicates, so \(4^4=\boxed{256}.\)

R    Y    G    B

1     1     1    1          Person 1 gets all 4  R Y G B

1     1     1    2       Person 1 gets  R Y G and person 2 gets B  (& Peeps 3 &4 get 0: No Bracelet)

.

.

.

.

.

4     4    4     4            where the numbers represent the person who gets the   R Y G B bracelet....

So there is   4 * 4 * 4 * 4  =256  combos 

                                   ( if a person is not reperesented by a number, it is zero: No Bracelet)

Rom answered this yesterday.......see your previous posting......

See here: https://web2.0calc.com/questions/hlelp-plzzz

Since AB = AC   the angles opposite these sides are equal

So m ABC =   [ 180 - m BAC] /2   =  [ 180 - 42 ] / 2  =  138/2 = 69°

And since ABC is an inscribed angle, then it intercepts an arc that is twice its measure

So  minor arc AC =  138°

And a chord meeting a tangent forms an angle =  1/2 the arc intercepted by the chord

So  chord AC intercepts minor arc AC....so....

m angle ACD  =  138 / 2  = 69°

We can start off by using the finding angle B. We have \(\frac{180-42}{2}=\frac{138}{2}=69^\circ\) . Now, by the tangent formula, the arc AC is twice angle B, so \(69*2=138^\circ\) . Now, finally the chord and tangent, we have \(\frac{1}{2}*138^\circ=\boxed{69^\circ}.\)

Isn't this an angle formed by a tangent and chord. If so, we have angle B and C as 180-42=138 divided by 2 equals 69. Since arc AC has the twice angle measure of angle B, we get 138. Learn this, pretty useful. Thus, angle ACD is 69 degrees. 

Note that  we can write

10!  [ 1 / (9! * 1! )  + 1 / (3!*7! )  + 1/ (5!*5!) + 1/ (7!*3!) + 1/(9!*1!) ]  =

10! / (9! * 1!) + 10! / (3!*7!) + 10! / (5!*5!) + 10! / (7!*3!) + 10!/(9!*1!)  

C(10, 1)  + C(10, 3) + C(10, 5)  + C(10,3) + C(10,1)  =

2 C(10, 1)  + 2 (10, 3) + C(10, 5)   =

20  + 240   +  252  =

512

So

10!  [ 1 / (9! * 1! )  + 1 / (3!*7!  + 1/ (5!*5!) + 1/ (7!*3!) + 1/(9!*1!) ]  =  512

[ 1 / (9! * 1! )  + 1 / (3!*7!  + 1/ (5!*5!) + 1/ (7!*3!) + 1/(9!*1!) ]  =  512 / 10!  =  2⁹ / 10!

(a , b)  =  (9, 10)

Should be better now, thanks. 

deleted

solution to what?

I get    2^9 / 10!       (a,b) = (9,10)