For a list of data, you would:
1) Find the average (mean) of all the data numbers. (Add all of the numbers, then divide by how many numbers there are in the list).
2) Take each number in the original data list and subtract that average number from each data number. Then, square the result. You should now have a new list of numbers.
3) Find the average of all the numbers in this new list.
4) Take the square root of that average, which is the standard deviation for that data.
This page can explain the process more clearly: http://www.mathsisfun.com/data/standard-deviation-formulas.html
As a side note, you can also use a calculator such as a TI-84 to calculate standard deviation. On the TI-84, enter the data as a list in "2nd" "LIST".
Then go to "2nd" "LIST" => "MATH" => "7stdDEV( " and press "Enter".
Then go to "2nd" "LIST" and select the list number. Press "Enter" and the standard deviation will show up.
SlicesThere are two main "slices" of a circle:
| 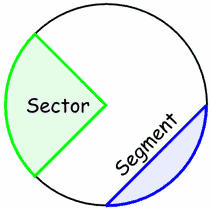 |
| Sector | Segment |
|---|---|
The Quadrant and Semicircle are two special types of Sector:
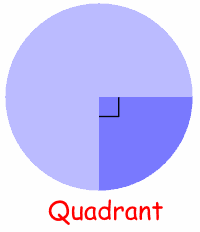 | Quarter of a circle is called a Quadrant. Half a circle is called a Semicircle. |
 |
Area of a SectorYou can work out the Area of a Sector by comparing its angle to the angle of a full circle. Note: I am using radians for the angles. | 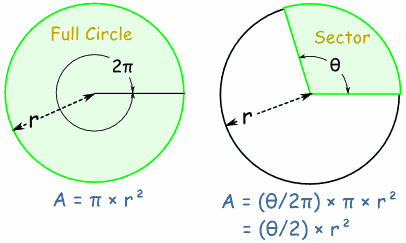 |
| This is the reasoning:
Area of Sector = ½ × θ × r2 (when θ is in radians) Area of Sector = ½ × (θ × π/180) × r2 (when θ is in degrees) | |
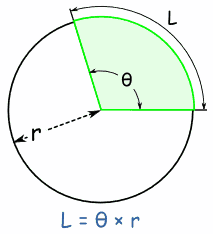 | Arc LengthBy the same reasoning, the arc length (of a Sector or Segment) is: L = θ × r (when θ is in radians) L = (θ × π/180) × r (when θ is in degrees) |
Area of SegmentThe Area of a Segment is the area of a sector minus the triangular piece (shown in light blue here). There is a lengthy reason, but the result is a slight modification of the Sector formula: | 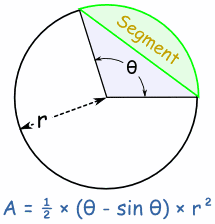 |
| Area of Segment = ½ × (θ - sin θ) × r2 (when θ is in radians) Area of Segment = ½ × ( (θ × π/180) - sin θ) × r2 (when θ is in degrees) | |