All Answers 354281 Answers

y  = sqrt  (ax + b)          square both sides

y^2  =  ax + b             subtract b from both sides

y^2 - b  =  ax            divide both sides by  a

y^2 / a  - b/a   =    x             "swap"  x  and y

x^2 / a  -  b/a   =   the inverse

So.....we have that

(1/a)x^2  -  b/a   =  -(a + 2)x^2  +  (2b + 1)

This must mean that

1/a   = -(a + 2)

1/a  = -a - 2

a + 1/a  + 2  = 0        multiply through by a    and rearrange

a^2 + 2a  + 1  =  0     factor

(a + 1)^2  =  0            take the root

a + 1   =   0

a  = -1

So.....we also have that

-b/a  = 2b + 1

-b/ (-1)  =  2b + 1

b  = 2b + 1

-1   = b

So  

a + b  = 

-1  +  -1   =

-2

We can find the time that it takes the ball to hit the ground  as follows :

-36.7  = (1/2) * -(9.8) * t^2

-36.7  = -4.9 * t^2

(36.7 /4.9)   = t^2    take the positive root

t ≈  2.74 sec

The x component of the velocity remains constant an can be found as

x  = v_x * t       

Where x is the horizontal displacement, v_x  is the horizontal component of the velocity and t is the time it takes the ball to hit the ground....so....

91.9  = v_x  * 2.74

91,9 / 2.74  = v_x  ≈  33.6 m / s

WooooHOOOOOO Let's go Nirvana and Hectitar!!!

Sorry to interrupt- did you say Hecker Nuggets?

Don't see  a figure, but I believe that we have three rectangles,  each with a height of 8 inches and a width of 10 inches....so the total area of the side panel is

3 * (8 *10)  =

3 * 80  =

240 square inches

Can Anyone Help????

Thanks for putting such effort into explaining that Hectictar :)

I expect Nirvana, more then most, will take full advantage of your time and explanation.

You are both great assets to this forum  

but if you can rotate it of reflect it to be the same, it is counted twice.

I have drawn something similar.

The 17 is exact but the 50 is not. 

I drew it in Geobebra and it has variables on a slider so the shape can be changed.

I actually do not think it should be that difficult to answer properly but I have not been sucessful

Thank you, sinclairdragon428 !

Thank you to everyone! 6300 is the answer, so special thanks to heureka

heureka: You counted 4,500 ODD digits. He/she wants "four-digit odd numbers", which is 5^4 =625 odd numbers.

heureka: Isn't the number of odd integers from the left: 5(1,3,5,7,9) x 5 x 5 x 5 =5^4 =625 such numbers.

let a equal the number of four digit odd numbers. let b equal the number of four digit multiples of 5. find a+b.

I assume:

These are two arithmetic series.

\(\begin{array}{|rcll|} \hline 1001 + (a-1)\cdot 2 &=& 9999 \quad | \quad \small \text{first odd four digit number }=1001,\ \text{last odd four digit number }=9999\\ (a-1)\cdot 2 &=& 9999 - 1001 \\ (a-1)\cdot 2 &=& 8998 \\ a-1 &=& 4499 \\ a &=& 4499+1 \\ \mathbf{a} &=& \mathbf{4500} \\\\ 1000 + (b-1)\cdot 5 &=& 9995 \quad | \quad \small \text{first four digit number multiples of 5}=1000,\ \text{last four digit number }=9995\\ (b-1)\cdot 5 &=& 9995 - 1000 \\ (b-1)\cdot 5 &=& 8995 \\ b-1 &=& 1799 \\ b &=& 1799+1 \\ \mathbf{b} &=& \mathbf{1800} \\ \hline \end{array} \)

\(a+b = 4500+1800 = 6300\)

There are: 5^4 = 625 odd integers

There are 9000 / 5 =1,800 multiple of 5 integers

900 + 625 =1525 Total integers

I just found it on the Internet.

thank you!

thanks!

How many paths are there from C to B, if every step must be up or to the right?

Find 1 + (1 + 2) + (1 + 2 + 3) + (1 + 2 + 3 + 4) + ... + (1 + 2 + 3 + ... + n).

\(\mathbf{s_n=\ ?}\)

\(\begin{array}{|lcccccccccc|} \hline \text{First row}: & \color{red}d_0=1 & &3 & &6 & &10 & & 15 & \ldots \\ \text{Second Row}: & &\color{red}d_1=2 & &3 & &4 & &5 & \ldots \\ \text{Third row}: & & &\color{red}d_2=1 & &1 & & 1& \ldots \\ \hline \end{array} \)

\(\begin{array}{rcl} s_n &=& \dbinom{n}{1}\cdot {\color{red}d_0 } + \dbinom{n}{2}\cdot {\color{red}d_1 } + \dbinom{n}{3}\cdot {\color{red}d_2 }\\ s_n &=& \dbinom{n}{1}\cdot {\color{red}1 } + \dbinom{n}{2}\cdot {\color{red}2} + \dbinom{n}{3}\cdot {\color{red}1}\\ \\ \hline \binom{n}{1} &=& n \\ \binom{n}{2} &=& ( \dfrac{n}{2} ) \cdot ( \dfrac{n-1}{1} ) \\ \binom{n}{3} &=& ( \dfrac{n}{3} ) \cdot ( \dfrac{n-1}{2} )\cdot ( \frac{n-2}{1} ) \\ \hline \\ s_n &=& (n)\cdot {\color{red}1} + ( \dfrac{n}{2} ) \cdot ( \dfrac{n-1}{1} )\cdot {\color{red}2} + ( \dfrac{n}{3} ) \cdot ( \dfrac{n-1}{2} )\cdot ( \dfrac{n-2}{1} )\cdot {\color{red}1} \quad | \quad \cdot 6\\ \\ 6\cdot s_n &=& n\cdot 6 + n \cdot ( n-1 )\cdot 6 + n \cdot ( n-1 )\cdot ( n-2 ) \\ 6\cdot s_n &=& n \left[~ 6 + ( n-1 )\cdot 6 + ( n-1 )\cdot ( n-2 ) ~\right] \\ 6\cdot s_n &=& (n) \left(~ 6 + 6n-6 + n^2 - 3n + 2 ~\right) \\ 6\cdot s_n &=& (n) \left(~ n^2 + 3n + 2 ~\right) \\ 6\cdot s_n &=& (n) \cdot (n+1) \cdot ( n+2 ) \\\\ \mathbf{s_n} &=& \mathbf{ \dfrac{ n \cdot (n+1) \cdot ( n+2 ) }{6} } \qquad \text{or} \qquad \mathbf{s_n} = \dbinom{n+2}{3} \\\\ s_1 &=& 1 = \dfrac{ 1 \cdot 2 \cdot 3}{6} = 1\\ s_2 &=& 1+3 = \dfrac{ 2 \cdot 3 \cdot 4 }{6} = 4 \\ s_3 &=& 1+3+6 = \dfrac{ 3 \cdot 4 \cdot 5 }{6} = 10 \\ s_4 &=& 1+3+6+10 = \dfrac{ 4 \cdot 5 \cdot 6 }{6} = 20\\ s_5 &=& 1+3+6+10+15 = \dfrac{ 5 \cdot 6 \cdot 7 }{6} = 35\\ \cdots \end{array}\)

For a certain value of r, the system

     x + y + 3z = 10, 

-4x + 2y + 5z = 7, 
            rx + z = 3
has no solutions. What is this value of r?

There is no solution, if the determinant \(\begin{vmatrix} 1&1&3\\-4&2&5\\r&0&1\end{vmatrix} = 0 \)

\(\begin{array}{|rcll|} \hline \begin{vmatrix} 1&1&3\\-4&2&5\\r&0&1\end{vmatrix} &=& 0 \\ 1\cdot2\cdot1+r\cdot1\cdot5+(-4)\cdot0\cdot3-r\cdot2\cdot3-(-4)\cdot1\cdot1-1\cdot5\cdot0 &=& 0 \\ 2+5r+0-6r+4-0&=& 0 \\ 6-r &=& 0 \\ \mathbf{r} &=& \mathbf{6} \\ \hline \end{array} \)

Camy made a list of every possible distinct five-digit positive integer that can be formed using each of the digits 1, 3, 4, 5 and 9 exactly once in each integer. What is the sum of the integers on Camy's list?

I assume, we count the numbers of all permutations of 13459.

The sum is:

\(\begin{array}{|rcll|} \hline && \dfrac{5!}{5} \times (1+3+4+5+9)\times (10^0+10^1+10^2+10^3+10^4) \quad | \quad 5!=120 \\ &=& \dfrac{120}{5} \times 22\times 11111 \\ &=& 24 \times 22\times 11111 \\ &=&\mathbf{ 5 866 608 } \\ \hline \end{array} \)

The sum of the integers on Camy's list is 5866608

We put one open curly brace beside the "pieces" of the piecewise function, for example:

\(f(x)=\begin{cases} x+2 & \text{if}&x> 2 \\ x^2 &\text{if}& -3< x\leq 2 \\ 9 &\text{if}& x\leq-3 \end{cases}\)

This is the way to show the pieces of a piecewise function.

On the other hand, domains and ranges (and, of course, intervals) can be expressed in interval notation.

An interval is a set of values or numbers - not a set of expressions or functions.

E.g., the interval  [0, 5)  is every number between  0  and  5, including 0 and excluding 5.

And by looking at the graph for this function:

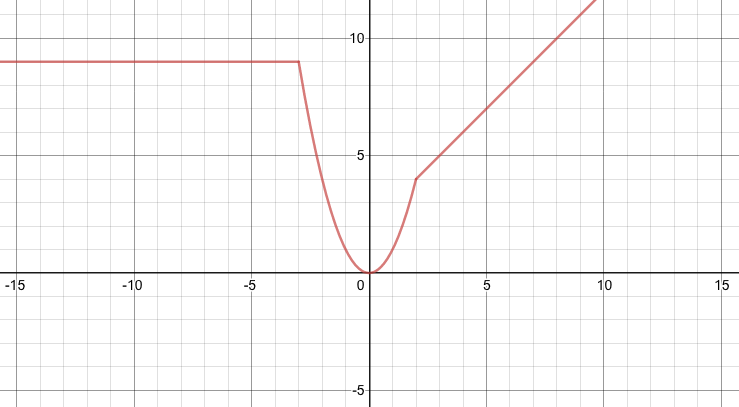
We can see:

All of those are intervals expressed in interval notation.

(At the points where  x = 2  and  x = -3 ,  the slope is undefined, and so the function is neither increasing nor decreasing, and so we do not include those values in the intervals of increase or decrease.)

Mmm, your right, Mine is just one possible answer, with regards to the diagonal lengths, and it certainly does not need to be a rectangle. 

Plus I failed to account for the fact that all side lengths are integer.

So in short, mine is wrong.

Did you draw that pic or was it given to you?

In the diagram below, points A, B, C, and P are situated so that PA=2, PB=3, PC=4, and BC=5.
What is the maximum possible area of \(\triangle ABC\)?

\(\text{Let $\triangle BPC = 90^\circ$ } \\ \text{Let $\triangle BPA = \alpha$ } \\ \text{Let $\triangle CPA = 270^\circ-\alpha$ } \\ \text{Let $ A_1 = \text{area }\triangle BPA$ } \\ \text{Let $ A_2 = \text{area }\triangle CPA$ } \\ \text{Let $ A_3 = \text{area }\triangle BPC=\dfrac{3\cdot 4}{2}= 6 $ } \\ \)

\(\begin{array}{|lrcll|} \hline & A_1 &=& \dfrac{2\cdot 3 \cdot \sin(\alpha)}{2} \\ (1) & A_1 &=& 3 \cdot \sin(\alpha) \\\\ & A_2 &=& \dfrac{2\cdot 4 \cdot \sin(270^\circ-\alpha)}{2} \\ & A_2 &=& 4 \cdot \sin(270^\circ-\alpha) \quad | \quad \sin(270^\circ-\alpha) = -\cos(\alpha) \\ (2) & A_2 &=& -4 \cdot \cos(\alpha) \\ \hline & f(\alpha) &=& A_1+A_2 \\ & &=& 3 \sin(\alpha)-4 \cos(\alpha) \\ & f'(\alpha) &=& 3 \cos(\alpha)+4 \sin(\alpha) = 0 \\ & 3 \cos(\alpha)+4 \sin(\alpha)& =& 0 \\ & 4 \sin(\alpha)& =& -3 \cos(\alpha) \\ & \tan(\alpha)& =& -\dfrac{3}{4} \\ & \alpha &=& \arctan \left(-\dfrac{3}{4} \right) +180^\circ\\ & \alpha &=& -\arctan (\dfrac{3}{4}) +180^\circ\\ & \alpha &=& -36.8698976458 +180^\circ\\ &\mathbf{ \alpha } &=& \mathbf{143.130102354^\circ \quad | \quad \text{area }(A_1+A_2)_{\text{max.}} }\\ \hline \end{array}\)

Area of  \(\triangle ABC_{\text{max.}}\)

\(\begin{array}{|rcll|} \hline A_{\text{max.}} &=& A_1+A_2+A_3 \\ &=& 3 \sin(\alpha)-4 \cos(\alpha) + \dfrac{3\cdot 4}{2} \\ &=& 3 \sin(143.130102354^\circ)-4 \cos(143.130102354^\circ) + \dfrac{3\cdot 4}{2} \\ &=& 3\cdot (0.6) -4\cdot (-0.8) + 6 \\ &=& 1.8 + 3.2 + 6 \\ &=& 5 + 6 \\ \mathbf{A_{\text{max.}}} &=& \mathbf{ 11 } \\ \hline \end{array}\)

The maximum possible area of \(\triangle ABC =11\)