See the image here
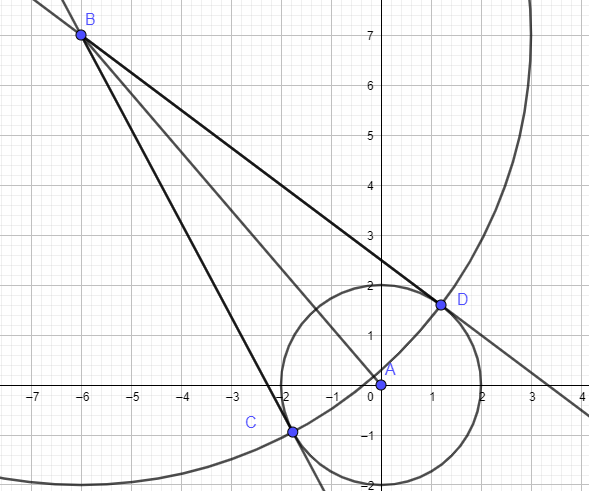
The two lines will be tangent to the circle with the equation x^2 + y^2 = 4
The radius of this circle, and each tangent line will form legs of two congruent right triangles with AB the hypotenuse of both
A = (0,0) B = (-6,7)
AC = AD = 2 AB =sqrt ( 6^2 + 7^2) = sqrt (85)
So
AB^2 - AC^2 = BC^2
85 - 4 = BC^2
81 = BC
9 = BC = BD
If we draw a circle with radius = 9 centered at (-6,7) we have
(x + 6)^2 + (y - 7)^2 = 81
x^2 + 12x + 36 + y^2 - 14y + 49 = 81
X^2 + y^2 + 12x - 14y = -4
4 + 12x - 14y = -4
12x - 14y = -8
6x - 7y = -4
7y = 6x + 4
y= (6x + 4) / 7
Sub the last equation into x^2 + y^2 = 4 and we will find the x intercepts of the tangent lines with the circle x^2 + y^2 = 4
x^2 + ( 6x + 4)^2 /49 = 4
Solving this produces x = -30/17 and x = 6/5
And when x = -30/17, y = -16/17 = C
And when x = 6/5 , y = 8/5 = D
Slope of BC = (7 - -16/17) / ( -6 - -30/17) = (7 + 16/17) /( -6 + 30/17) = -15/8
Slope of BD = (7 - 8/5) /( -6 - 6/5) = -3/4 = - 6/8
Sum of the slopes = -15/8 - 6/8 = - 21 / 8


