Note that    sqrt (x^2)  can be defined as   l x l

The range of this  function is  [ 0, inf)

Could there also be some complex numbers involved here?

Let the first term  = n

Let the third  =  n + 2d

So

n (n + 2d)  =  9

We have two  different (positive) factors that multiply to 9  →  1  and  9  

So  if   n =  1     and  d = 4   then

1 ( 1 + 8)  = 9

1 (9)  = 9

So the 4th term is    1 + 4(4 -1)  =  1 + 12  =  13

A and B could both be winners in the first match, and C and D could both be winners of the second match.

So really, all combinations of A, B, C and D are possible rankings here, given there are no tied matches.

So we are back to square one, in how many ways can You order the four teams A, B, C and D?

Lets look at the first possibility, that team A comes out on top, then we have these possible rankings:

A>B>C>D

A>B>D>C

A>C>B>D

A>C>D>B

A>D>B>C

A>D>C>D

This gives us 6 possible combinatioons with A as the winners. The same is true if either of the other

teams win, so we have 6 x 4 rankings = 24.

We can calculate this number by taking the faculty of 4, 4! = 4 x 3 x 2 x 1 = 24

Thank You, Alan. It was late, and I must have made some simple error somewhere.

A bit of vector algebra. But really only the pythagorean theorem.

We can find the vectors for each diagonal by subtracting startpoint from endpoint, so

AC = (12,-2) - (0,7) = (12-0, -2-7) = (12,-9)

BD = (7,8) - (1,0) = (7-1, 8-0) = (6,8)

We can find the length of each of these by taking the square of each vector component, add

them togehter and then taking the square root of this sum.

So the length of AC, denoted |AC| = \(\sqrt{12\times12 + (-9)\times(-9)} = \sqrt{144 + 81} = \sqrt{225} = 15\)

Similarly, the length of BD,  |BD| = \(\sqrt{6\times6 + (8)\times(8)} = \sqrt{36 + 64} = \sqrt{100} = 10\)

The rule for finding the Area of the kite is 1/2 x |AC| x |BD| = 1/2 x 15 x 10 = 1/2 x 150 = 75

Hope this helps.

Very nice, Tuffla  !!!

Welcome aboard, Tuffla!!

Here's one  more way

Let him start  at (0,0)

When he walks 800 feet west he is at  (-800, 0)

When he then  walks 900 ft due north he is at  (-800 , 900)

When he then walks 1500 ft due east he is at  ( -800 + 1500, 900) = (700,900)

When he walks due south 100 ft he is at ( 700 , 900 - 100) =  (700, 800)

And his distance from the starting  point (as Tuffla calculated)  is   

sqrt [ 700^2 + 800^2 ]  =

sqrt [ 100^2  ( 7^2 + 8^2) ]  =

100 sqrt [ 113  ]  ft   ≈   1063 ft

Assuming  a box could be empty

Choose all 5 balls to go into  either box  - the other box is empty by default

C(5,5) * 2             =    2 ways

Choose  4 of the 5 balls to go into either box  -  the remaing ball goes into the other box by default

C(5,4)  *2            =    10   ways

Choose 3 of the 5 balls  to go into either box -  the remaining two balls go into  the other box by default

C(5,3) * 2             =   20 ways

32 ways 

The eighth  row of Pascal's Triangle  produces

1   8    28   56  70  56   28   8    1

The only   odd terms will   be  1m^8   and 1n^8  since the multiplication of any product by an even produces an  even

So.....two terms will be odd

As follows:

I get the following:

(Check your calculation "So the second term now evaluates to (-10/9)/(181/100) = -1,000/729" tuffla2022)

As follows:

The heigh of the parallellogram is 1/2 x 14, or 7, so the area becomes 10 x 7 = 70. Try and draw it, and You will see that there is a 30-60-90 triangle, where BC is the hypothenus, so the shortest side in this triangle becomes half the length of the hypothenus, that is 7. This is the height of the parallellogram.

Well, how many balls can be placed in each box?

\(f(x) = x^{-1} + \frac{x^{-1}}{1+x^{-2}}\)

I think this looks a little better:

\(f(x) = \frac{1}{x} + \frac{\frac{1}{x}}{1+\frac{1}{x^2}}\)

Let's first find f(-2):

\(f(-2) = \frac{1}{-2} + \frac{\frac{1}{-2}}{1+\frac{1}{(-2)^2}}\)

we can simplify this somewhat, since the denominator in the second term is

1 + 1/4 = 5/4, and so the second term becomes - 4/10 or -2/5

f(-2) = -1/2 - 2/5 = -5/10 - 4/10 = - 9/10

Next we must find f(-9/10):

\(f(\frac{-9}{10}) = \frac{1}{\frac{-9}{10}} + \frac{\frac{1}{\frac{-9}{10}}}{1+\frac{1}{(\frac{-9}{10})^2}}\)

The first term evaluates to -10/9, ans so does the numerator in the second term.

The denominator is 1 + 1/(81/100), or 1 + 100/81, that is 181/81.

So the second term now evaluates to (-10/9)/(181/100) = -1,000/729

The sum of the two terms is -10/9 - 1,000/729 = -810/729 - 1,000/729 = -1,810/729 or -2 -352/729.

That is, if my calculations are correct... This was quite an excercise, so maybe I'm wrong somewhere...

The domain is all real numbers

The range is all real numbers greater or equal to 0

I think it is 13. In an Arithmetic Sequence the difference between one term and the next is a constant.

So if we imagine the first number is 1 and then the third is 9, we have these three numbers 1, 5, 9...

We see that there is a jump of 4 every time, so the sequence becomes...

1, 5, 9, 13, 17, 21 ....

For x<1, we have that f(x) = 2 - x.

We calculate the inverse by first setting f(x) = y, then solve for x

y = 2 - x, -x = y-2, x = 2 - y

so k(x) = 2 - x, and f(x) = 2 -x in the whole of R

The drawing from GeoGebra online shows that the mirror image og f(x) axross the line y = x is it's inverse function, k(x), which in this case has the same definition as f.

This is probably pre vector algebra or something.

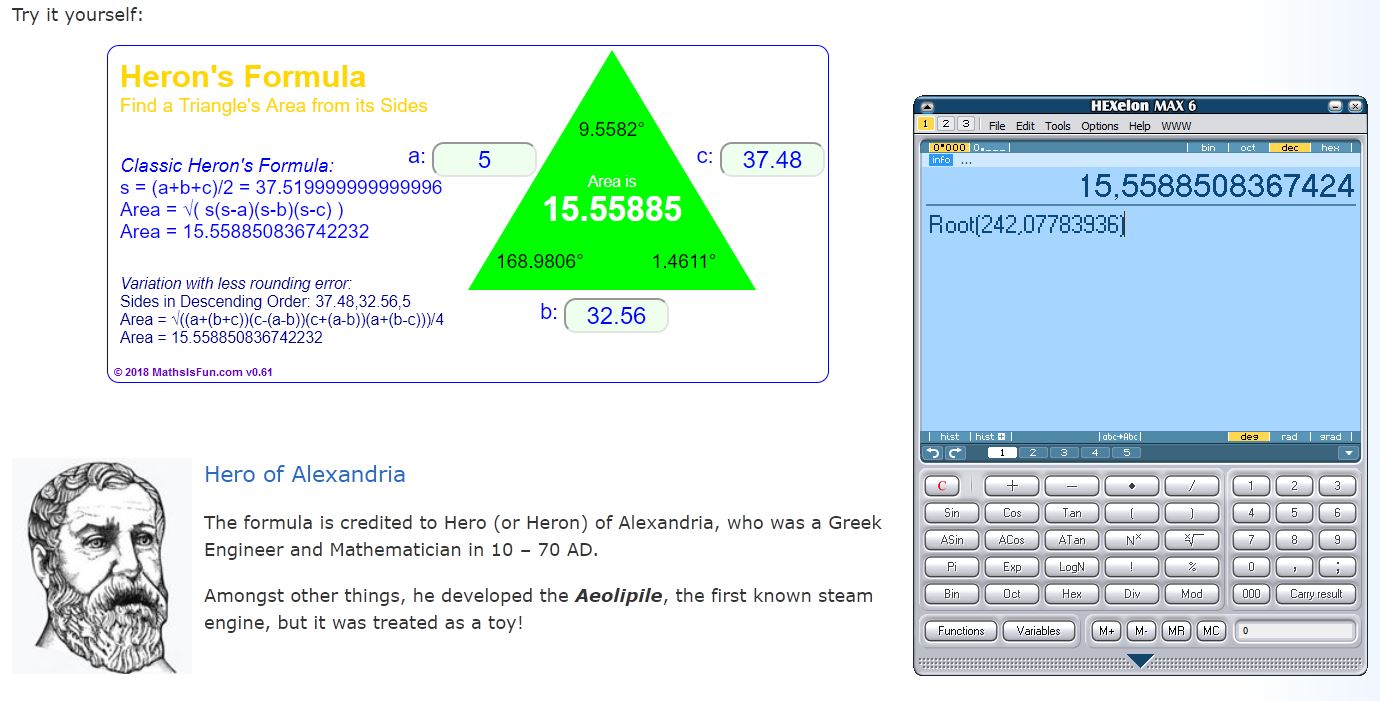
Let's call these vertices A(1,6), B(1,11) and C(7,43).

We can find the length of each of the sides using the pythagorean theorem.

AB = (0,5), length = 5

AC = (6,37), length = \(\sqrt{6^2 + 37^2} = \sqrt{1,405} \approx 37.48\)

BC = (6,32), length = \(\sqrt{6^2 + 32^2} = \sqrt{1,405} \approx 32.56\)

By stars-and-bars, there are 15 ways.

Is we assume these books are all different, we can call the books A, B, C and D.

You can start lining up the possibilities. Let's start with book A:

A -> B -> C -> D

A -> B -> D -> C

A -> C -> B -> D

A -> C -> D -> B

A -> D -> B -> C

A -> D -> C -> B

There are 6 different ways to go through these books starting with book A.

The same is true if we start with any other book. So there are 6 x 4 = 24 choices for the order he can read the books.

We use a formula for this kind of permutations problem:

Number of permutations: n! (n faculty) = n * (n-1) x (n-2) x ... x 2 x 1

For only 4 books there are 4 x 3 x 2 x 1 = 24 choices.

For 6 books there would have been: 6! = 6 x 5 x 4 x 3 x 2 x 1 = 720 choices.

It helps to draw this, using some drawing app.. GeoGebra online is fine for this sort of thing.

We can calculate the length EA by EA = \(\sqrt{EF^2 + FA^2} = \sqrt{700^2 + 800^2} = \sqrt{490,000 + 640,000} = \sqrt{1,390,000} = 1,063.015\)

Now we round this off to whole feet. He is 1,063 feet from where he started.

0.4 inches is 5 miles, so 1 inch equals 5/0.4 inches = 50/4 inches = 12.5 miles.

So 2 miles must be 2 x 12.5 miles = 25 miles.

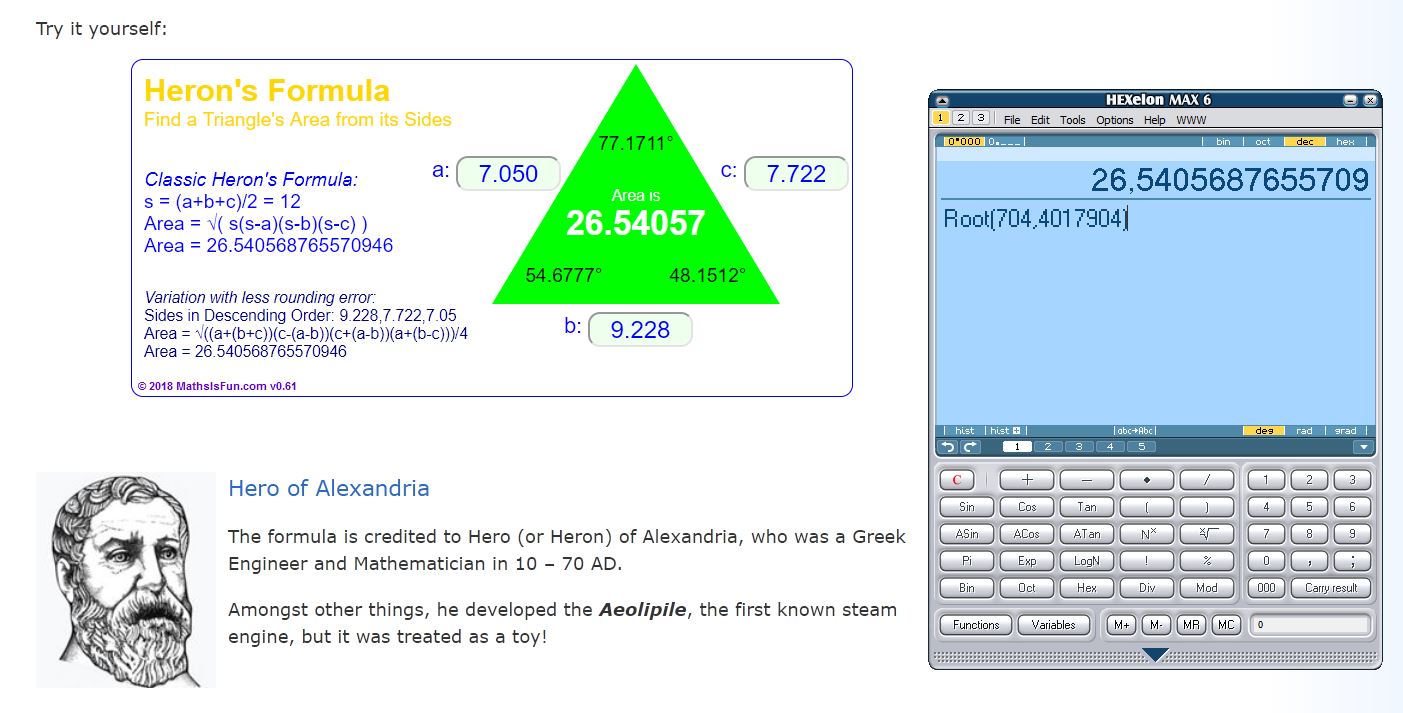
Find angle A = cos^-1(2/3) = 48.19 (Deg), and angle B = cos^-1(2/9) = 77.16 (Deg), so angle C = 180 - 48.19 - 77.16 = 54.65 (Deg).

The Sine Rule states that a/sin(A) = b/sin(B) = c/sin(C). We also know that a + b + c = 24.

Let's try and use both of these to express a and b by means of c.
a = c x (sin(A)) / sin(C) = c * 0.745 / 0.816 = 0.913 x c, b = c x (sin(B)) / sin(C) = c x 0.975 / 0.816 = 1.195 x c.

Substituting (exchanging) a and b for these gives us that: a + b + c = 24 is the same as 0.913 c + 1.195 c + c = 24,
or 3.108 c = 24. Divding on both sides gives us c = 24 / 3.108 = 7.722.

Now we can back-substitute and find a and b, a = 0.913c = 0.913 x 7.722 = 7.050, and b = 1.195c = 1.195 x 7.722 = 9.228.