+118723

I gave Chris 3 points :)

We rarely get mad with each other and we NEVER stay mad for long :)

Yes Heather, I agree with you LOL

Hi Zegroes :)

MelodyApr 30, 2015

+118723

Where is your working zegroes. (ﾉ °益°)ﾉ彡 ┻━┻

MelodyApr 30, 2015

+118723

$$\\( 48a^{8}b^{25} )^{(1/4)}\\
=48^{1/4}a^{8*1/4}b^{25*1/4} \\
=16^{1/4}*3^{1/4}a^{2}b^{25/4} \\
=2\sqrt[4]{3}a^{2}b^{6.25} \\$$

That is not exactly simple but it is equivalent

MelodyApr 30, 2015

+26400

+13

$$\mathbf{12\binom{3}{3} + 11\binom{4}{3} + 10\binom{5}{3} + \cdots + 2\binom{13}{3} +\binom{14}{3} = \;?}$$

$$\small{\text{$
\begin{array}{l}
\mathbf{
12\binom{3}{3} +
11\binom{4}{3} +
10\binom{5}{3} +
9\binom{6}{3} +
8\binom{7}{3} +
7\binom{8}{3} +
6\binom{9}{3} +
5\binom{10}{3} +
4\binom{11}{3} +
3\binom{12}{3} +
2\binom{13}{3} +
1\binom{14}{3} } \\ \\
=
\mathbf{
\binom{4}{4} +
\binom{5}{4} +
\binom{6}{4} +
\binom{7}{4} +
\binom{8}{4} +
\binom{9}{4} +
\binom{10}{4} +
\binom{11}{4} +
\binom{12}{4} +
\binom{13}{4} +
\binom{14}{4} +
\binom{15}{4}
}\\\\
=
\mathbf{
\binom{16}{5}
}\\\\
=
\mathbf{
\dfrac{16!}{5!\cdot 11!}
}\\\\
=
\mathbf{
\dfrac{12\cdot 13\cdot 14\cdot 15\cdot 16}{5!}
}\\\\
=
\mathbf{
\dfrac{12\cdot 13\cdot 14\cdot 15\cdot 16}{1\cdot 2\cdot 3\cdot 4\cdot 5}
}\\\\
=
\mathbf{
\left(\dfrac{12}{3}\right)\cdot 13 \cdot
\left(\dfrac{14}{2}\right)\cdot
\left(\dfrac{15}{5}\right)\cdot
\left(\dfrac{16}{4}\right)
}\\\\
=
\mathbf{4 \cdot 13 \cdot 7 \cdot 3 \cdot 4}\\\\
=
\mathbf{13 \cdot 16 \cdot 21}\\\\
=
\mathbf{4368}
\end{array}
$}}$$

see Hockey Stick Pattern: http://ptri1.tripod.com/

If a diagonal of numbers of any length is selected starting at any of the 1's bordering the sides of the triangle and ending on any number inside the triangle on that diagonal, the sum of the numbers inside the selection is equal to the number below the end of the selection that is not on the same diagonal itself. If you don't understand that, look at the drawing.
1+6+21+56 = 84
1+7+28+84+210+462+924 = 1716
1+12 = 13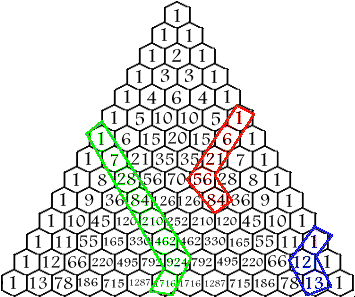

heurekaApr 30, 2015

Du hast vergessen die Lösungsvorschläge anzugeben. z.B. 2/3 davon oder 13/12.

Die Antwort ist 28/20. Das sollte einer der Lösungsverschläge sein. Man soll herrausfinden, bei welcher Bruchrechnung man besser bei weg kommt.

GuestApr 30, 2015

+26400

+10

$$\[\binom50+\binom51+\binom62+\binom71+\binom83+\binom92+\binom{10}4+\binom{11}3\] = 495$$

see: http://web2.0calc.com/#binom(5,0)+binom(5,1)+binom(6,2)+binom(7,1)+binom(8,3)+binom(9,2)+binom(10,4)+binom(11,3) and push the "=" Button

$$\small{\text{
$
\begin{array}{cccccccccccccccccccccccccc}
&&&&&&&&&&&\begin{pmatrix} 0\\0\end{pmatrix}=1\\
&&&&&&&&&&\begin{pmatrix} 1\\0\end{pmatrix}=1&&
\begin{pmatrix} 1\\1\end{pmatrix}=1\\
&&&&&&&&&\begin{pmatrix} 2\\0\end{pmatrix}=1&
&\begin{pmatrix} 2\\1\end{pmatrix}=2&
&\begin{pmatrix} 2\\2\end{pmatrix}=1\\
&&&&&&&&\begin{pmatrix} 3\\0\end{pmatrix}=1&&
\begin{pmatrix} 3\\1\end{pmatrix}=3&&
\begin{pmatrix} 3\\2\end{pmatrix}=3&&
\begin{pmatrix} 3\\3\end{pmatrix}=1\\
&&&&&&&\begin{pmatrix} 4\\0\end{pmatrix}=1&
&\begin{pmatrix} 4\\1\end{pmatrix}=4&
&\begin{pmatrix} 4\\2\end{pmatrix}=6&
&\begin{pmatrix} 4\\3\end{pmatrix}=4&
&\begin{pmatrix} 4\\4\end{pmatrix}=1\\
&&&&&&\begin{pmatrix} 5\\0\end{pmatrix}=1&&
\begin{pmatrix} 5\\1\end{pmatrix}=5&&
\begin{pmatrix} 5\\2\end{pmatrix}=10&&
\begin{pmatrix} 5\\3\end{pmatrix}=10&&
\begin{pmatrix} 5\\4\end{pmatrix}=5&&
\begin{pmatrix} 5\\5\end{pmatrix}=1\\
&&&&&\begin{pmatrix} 6\\0\end{pmatrix}=1&
&\begin{pmatrix} 6\\1\end{pmatrix}=6&
&\begin{pmatrix} 6\\2\end{pmatrix}=15&
&\begin{pmatrix} 6\\3\end{pmatrix}=20&
&\begin{pmatrix} 6\\4\end{pmatrix}=15&
&\begin{pmatrix} 6\\5\end{pmatrix}=6&
&\begin{pmatrix} 6\\6\end{pmatrix}=1\\
&&&&\begin{pmatrix} 7\\0\end{pmatrix}=1&&
\begin{pmatrix} 7\\1\end{pmatrix}=7&&
\begin{pmatrix} 7\\2\end{pmatrix}=21&&
\begin{pmatrix} 7\\3\end{pmatrix}=35&&
\begin{pmatrix} 7\\4\end{pmatrix}=35&&
\begin{pmatrix} 7\\5\end{pmatrix}=21&&
\begin{pmatrix} 7\\6\end{pmatrix}=7&&
\begin{pmatrix} 7\\7\end{pmatrix}=1\\
&&&\begin{pmatrix} 8\\0\end{pmatrix}=1&
&\begin{pmatrix} 8\\1\end{pmatrix}=8&
&\begin{pmatrix} 8\\2\end{pmatrix}=28&
&\begin{pmatrix} 8\\3\end{pmatrix}=56&
&\begin{pmatrix} 8\\4\end{pmatrix}=70&
&\begin{pmatrix} 8\\5\end{pmatrix}=56&
&\begin{pmatrix} 8\\6\end{pmatrix}=28&
&\begin{pmatrix} 8\\7\end{pmatrix}=8&
&\begin{pmatrix} 8\\8\end{pmatrix}=1\\
&&\begin{pmatrix} 9\\0\end{pmatrix}=1&&
\begin{pmatrix} 9\\1\end{pmatrix}=9&&
\begin{pmatrix} 9\\2\end{pmatrix}=36&&
\begin{pmatrix} 9\\3\end{pmatrix}=84&&
\begin{pmatrix} 9\\4\end{pmatrix}=126&&
\begin{pmatrix} 9\\5\end{pmatrix}=126&&
\begin{pmatrix} 9\\6\end{pmatrix}=84&&
\begin{pmatrix} 9\\7\end{pmatrix}=36&&
\begin{pmatrix} 9\\8\end{pmatrix}=9&&
\begin{pmatrix} 9\\9\end{pmatrix}=1\\
&\begin{pmatrix} 10\\0\end{pmatrix}=1&
&\begin{pmatrix} 10\\1\end{pmatrix}=10&
&\begin{pmatrix} 10\\2\end{pmatrix}=45&
&\begin{pmatrix} 10\\3\end{pmatrix}=120&
&\begin{pmatrix} 10\\4\end{pmatrix}=210&
&\begin{pmatrix} 10\\5\end{pmatrix}=252&
&\begin{pmatrix} 10\\6\end{pmatrix}=210&
&\begin{pmatrix} 10\\7\end{pmatrix}=120&
&\begin{pmatrix} 10\\8\end{pmatrix}=45&
&\begin{pmatrix} 10\\9\end{pmatrix}=10&
&\begin{pmatrix} 10\\10\end{pmatrix}=1\\
\begin{pmatrix} 11\\0\end{pmatrix}=1&&
\begin{pmatrix} 11\\1\end{pmatrix}=11&&
\begin{pmatrix} 11\\2\end{pmatrix}=55&&
\begin{pmatrix} 11\\3\end{pmatrix}=165&&
\begin{pmatrix} 11\\4\end{pmatrix}=330&&
\begin{pmatrix} 11\\5\end{pmatrix}=462&&
\begin{pmatrix} 11\\6\end{pmatrix}=462&&
\begin{pmatrix} 11\\7\end{pmatrix}=330&&
\begin{pmatrix} 11\\8\end{pmatrix}=165&&
\begin{pmatrix} 11\\9\end{pmatrix}=55&&
\begin{pmatrix} 11\\10\end{pmatrix}=11&&
\begin{pmatrix} 11\\11\end{pmatrix}=1
\end{array}
$}}$$

$$\small{\text{
$
\binom50+\binom51+\binom62+\binom71+\binom83+\binom92+\binom{10}4+\binom{11}3= 1+5+15+7+56+36+210+165 = 495
$}}$$

heurekaApr 30, 2015

+980

$${{\mathtt{20}}}^{{\mathtt{5}}} = {\mathtt{3\,200\,000}}$$

zacismynameApr 30, 2015

#11

+1222

I think that is moderators work, to just use login in or anon, but...

I also think that is better if u just can use logging in...

Dbg4thebestApr 30, 2015

Easy 14.0127388535

GuestApr 30, 2015

+529

Consider common fractions such as ½ or ¾ , etc. We see that the top is the smaller number in common fractions.

Now,count the letters in these words: "numerator" and "denominator". Which word has the fewest letters? "Numerator" is the shorter word, in common fractions it's also the smaller number.

Finally, generalise this to all fractions, both proper and improper: the top number is always the numerator.

🍽 🍽 🍽 🍽

BadinageApr 30, 2015

+130511

Well...the first night, the two people will split the $135 room fee.....and they will split the cost of (1/5) of the $81 service fee and the $55 cleaning fee.

So each will pay (1/2)(135) + (1/5)(81 + 55) = $94.70

So ...2(94.70) = $189.40 total paid so far

This leaves $[811 - 189.40] = $621.60 to be shared by 5 people for the other 4 nights.

So.....each will pay 621.60/ 5 = $124.32

So the first two people pay $[94.70 + 124.32] apiece = $219.02

And the rest pay $124.32 apiece

Check .... 2(219.02) + 3(124.32) = $811

CPhillApr 30, 2015

+130511

If something decreases.....the "formula" is

([Old Value - New Value] / Old Value x 100)%

For example......something decreases from 10 to 8....so we have...

([10 - 8 ] / 10 x 100 )% =

(2 / 10 x 100)% =

(.20 x 100)% =

20% decrease

If something increases, we have

([New Value - Old Value ] / Old Value x 100)%

Let's say we have the opposite situation......something increases from 8 to 10 .....so we have

([10 - 8 ] / 8 x 100)% =

(2 / 8 x 100)% =

(.25 x 100)% =

25% increase

And there you are !!!

CPhillApr 30, 2015

(4)+2-2)/2=

6-2/2=

4/2=

GuestApr 30, 2015

+130511

-8(-4) - 7 =

32 - 7 =

CPhillApr 30, 2015

+130511

The nth tem of an arithmetic series is given by :

a_n = a₁ + d(n - 1) where a_n is the term we're looking for, a₁ is the first term of the series, d is the common difference between successive terms, and n is the number of terms of interest....so .....

The 12th term is given by :

a₁₂ = 40 -11(12-1) = 40 - 11(11) = 40 - 121 = -81

CPhillApr 30, 2015

+130511

(5sqrt(2) +1) ( 5sqrt(2) -1)) .....so we have.....

[5sqrt(2)]^2 - 1

25 * 2 - 1 =

50 - 1 =

CPhillApr 30, 2015

+130511

1. y = 180 - 12x

2. At ground level, y will = 0 ....so

0 = 180 - 12x add 12x to both sides

12x = 180 divide both sides by 12

x = 15 seconds

3. We have

250 = 12x divide both sides by 12

250 / 12 = x = about 20.83 seconds

CPhillApr 30, 2015

+190

385.

dasiyApr 30, 2015

66 is 75% of 88

GuestApr 30, 2015

7x=-43

x=-43/7

x=-6.75

GuestApr 30, 2015

+130511

+12

Look at the following graph, Mellie........https://www.desmos.com/calculator/9p3hhbrwl2

The graph of all the possible arrival times - in minutes after 5 PM - by both Alice and Bob is bounded by x = 0, y = 0 x= 60 and y = 60.

Let the x values in the graph be the number of minutes after 5 PM that Alice arrives at the party. And let the y values be the number of minutes after 5 PM that Bob arrives at the party. For example, at (0,0), both arrive at 5PM and at (60,60), both arrive at 6 PM. At (0, 45)....Alice arrives at 5PM and Bob arrives at 5:45 PM. At (22.5, 22.5), both arrive at 5:22:30. And at (45, 0), Alice arrives 45 minutes after 5 PM and Bob arrives exactly at 5 PM.

But, the times we are interested in lie beneath the graph of x + y ≤ 45.

And this area is bounded by x = 0, y = 0 and x + y ≤ 45 . And it equals 45^2 / 2 = 1012.5 sq units

Note that the area of the total possible arrival times = 60 x 60 = 3600 sq units

So....the probabilty that the sum of Alice's and Bob's arrival times after 5PM are less than 45 minutes =

1012.5 / 3600 = 9/32

CPhillApr 30, 2015

+3502

66...........

zegroesApr 30, 2015

+1197

+10

You can cancel out the 3n on the numerator and the denominator, leaving you with $${\frac{{\mathtt{1}}}{{\mathtt{n}}}}$$

DarkBlaze347Apr 30, 2015

+1197

Divide both sides by h to isolate b, and you get b=(A/h).

DarkBlaze347Apr 30, 2015

All Answers 358087 Answers

🍽 🍽 🍽 🍽

2 Online Users

Top Users

Sticky Topics