challenge accepted.
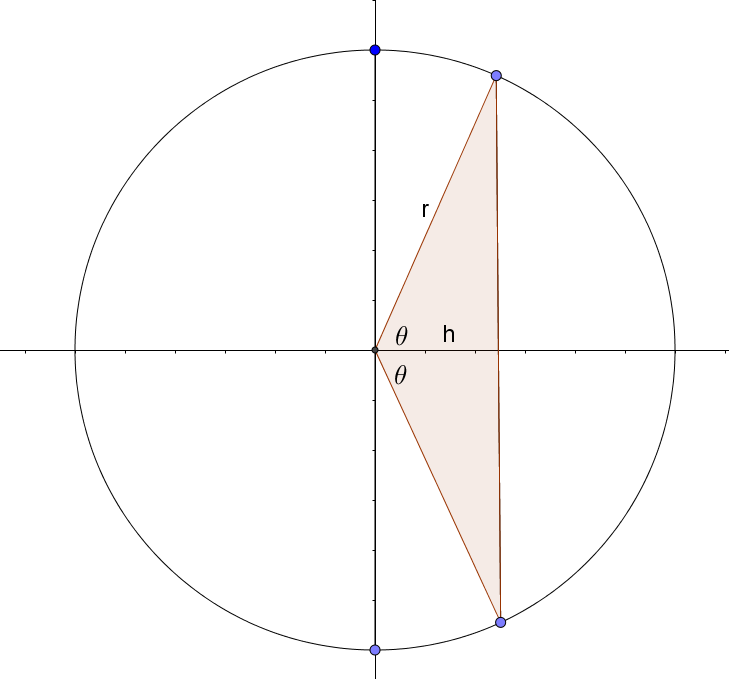
I am only looking at the semicircle on the right.
The coloured in brown bit plus the two little sectors must be half the size of the segment on the far right.
\(cos\theta = \frac{h}{r}\\ h=rcos\theta\\ Area\;of\;brown\; triangle=0.5r^2sin(2\theta)\\ Area \;of\;one\;little\;sector=\frac{(0.5\pi-\theta)}{2\pi}\pi r^2=\frac{(0.5\pi-\theta)r^2}{2}\\ \text{add these three areas together and get}\\ \text{half of middle slice is }\\ 0.5r^2sin(2\theta)+2*\frac{(0.5\pi-\theta)r^2}{2}\\ =0.5r^2sin(2\theta)+(0.5\pi-\theta)r^2\\ =r^2[0.5sin(2\theta)+0.5\pi-\theta]\\~\\ \text{area of segment }=0.5\pi r^2-r^2[0.5sin(2\theta)+0.5\pi-\theta]\\ \text{area of segment }=r^2[0.5\pi-0.5sin(2\theta)-0.5\pi+\theta]\\ \text{area of segment }=r^2[\theta-0.5sin(2\theta)]\\~\\ r^2[\theta-0.5sin(2\theta)]=2*r^2[0.5sin(2\theta)+0.5\pi-\theta]\\ \theta-0.5sin(2\theta)=sin(2\theta)+\pi-2\theta\\ 3\theta-1.5sin(2\theta)=\pi\\ \)
https://www.wolframalpha.com/input/?i=3x-1.5*sin(2x)%3Dpi++++++++++radians
\(\theta \approx 1.30266\;radians\)
\(h=rcos\theta\\ h\approx 0.2649r\)
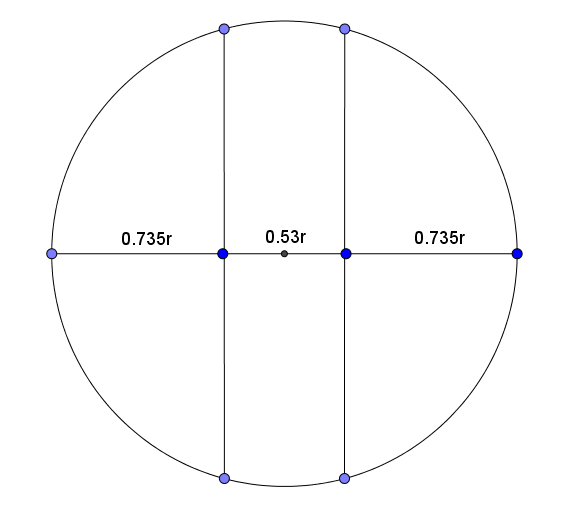
Here is what your Pizza should look like. The measurements are of course approximate.