It has been a long time since I have done questions like this but this is what I think.
n=81 p=0.477 q=1-p = 0.523
expected number of 1s and 2s in 81 invoices is np = 81*0.477=38.637
\(\bar x=38.637\)
\(\sigma ^2= npq\\ \sigma ^2= 81*0.477*0.523\\ \sigma ^2= 20.2072\\ \sigma = 4.4952\\\)
Now there were 25 ones and twos. This is below the expected mean of 38.637
38.637-25=13.637 It is below by this many in actual number but how many standard deviations below it is?
13.637/4.4952 = 3.0336803701726286
Mmm it is 3.0337 standard deviations below the expected mean.
I think the probability of there being 25 or less ones or twos is 0.0012 or 0.12%
http://onlinestatbook.com/2/calculators/normal_dist.html
So it seems likely there is some fraud happening here.
I used this site to help me muddle through this question.
Accept my answer at your peril :)
Here is a very old post that you may find very helpful.
The original question is a little different from yours so be a little patient with looking at the answers :)
https://web2.0calc.com/questions/it-just-doesn-t-make-sense-to-me
Actually, if you scroll the the very bottom of this thread you will find there is another link.
You may like it even more :) It is more attractively presented ![]()
For those of you who wonder how I found these, (they are over 3 years old)
They are in the reference material thread that is in the Sticky Topics :)
Here is the problem explained
https://www.youtube.com/watch?v=SC5CX8drAtU
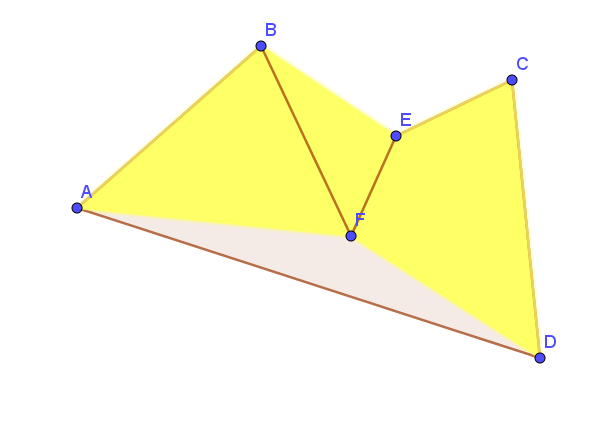
I think the trick is to make the route the thinest polygon possible, (So no cross overs of the route)
So for the 6 cities below I think the shortest route would be to work your way around the yellow hexagon. This is of course if you are flying directly between the cities. ![]()