Hi FencingKat,
I have been asked if I can show or prove this without using calculus. So here goes ....
Prove that
\(\sqrt{ \frac{2x^2 - 2x + 1}{2} } \ge \frac{1}{x + \frac{1}{x}}\qquad for \quad 0
-----------------------------------------------------------------------
First I will consider the LHS, I am going to look at it bit by bit.
For the LHS to be real
\(2x^2-2x+1\ge0\)
consider
\(y=2x^2-2x+1 \\ \)
This is a concave up parabola so it will be negative between the roots.
First find the roots.
\(2x^2-2x+1 =0\\ x=\frac{2\pm\sqrt{4-8}}{4} \)
there are no solutions to this so the roots are imaginary.
This parabola is always above the x axis
\(2x^2-2x+1>0 \;\;for\;\;all\;\;real\;\;x \\ \)
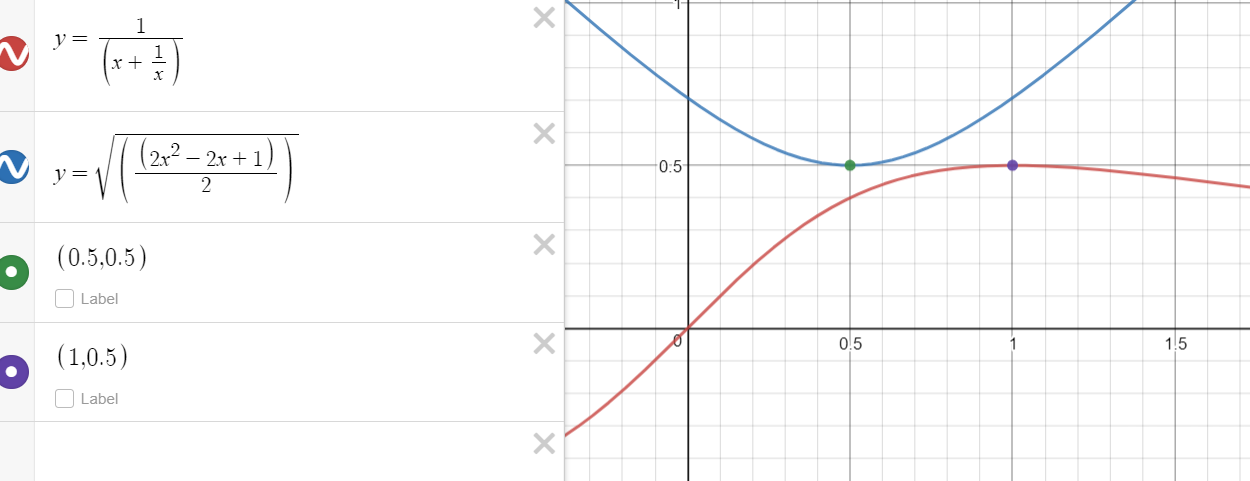
The minimum value is at x=1/2 and it is
2*0.5^2-2*0.5+1 = 0.5
so for 0
\(\text{minimum value of }\sqrt{\frac{2x^2-2x+1}{2}}=\sqrt{\frac{0.5}{2}}=\frac{1}{2} \)
------------------------------------------------------------
Now consider the RHS
\(RHS = \frac{1}{x+\frac{1}{x}} \\\text{As x approaches } 0^+ \text{ the RHS approaches 0}\\ \text{As x approaches 1 the RHS approaches }\frac{1}{2}\)
Now I suspect that the RHS is never more than 0.5 in the given domain
so i am going to determine for what values of x is the RHS less then or equal to 0.5
\(\frac{1}{x+\frac{1}{x}}\le\frac{1}{2}\\ 2 \le x+\frac{1}{x}\\ 2x \le x^2+1\\ 0 \le x^2-2x+1\\ x^2-2x+1\ge0\\ \triangle=b^2-4ac=4-4=0\\ \text{There is only 1 root (which we already know is when x=1)}\\ \text{plus } y=x^2-2x+1 \text{ is a concave up parabola so }\\ \frac{1}{x+\frac{1}{x}}\le\frac{1}{2} \text{ for all positive real x} \)
So the maximum of the RHS is 0.5 and that occurs when x=1
and the minimum of LHS is 0.5 and that occurs when x= 0.5
so thereforeLHS is not just greater or equal to RHS for all x between 0 and 1
I can go further and say that
LHS is greater than RHS for all all real x greater than 0.
so it is proven that
\(\sqrt{ \frac{2x^2 - 2x + 1}{2} } \geq \frac{1}{x + \frac{1}{x}}\qquad for \quad 0
it is also proven that
\(\sqrt{ \frac{2x^2 - 2x + 1}{2} } > \frac{1}{x + \frac{1}{x}}\qquad for \quad x>0\)
Here is a pic