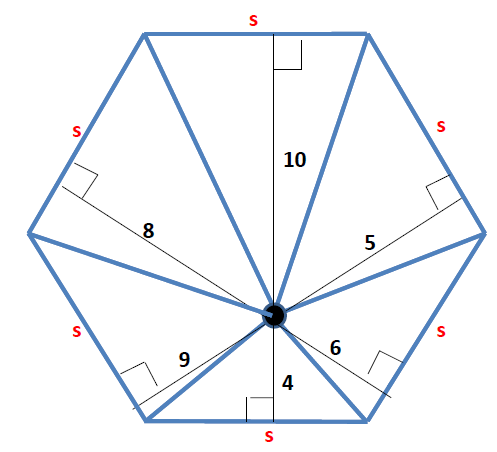
The lengths of the perpendiculars drawn to the sides of a regular hexagon from an interior point are 4, 5, 6, 8, 9, and 10 centimeters.
What is the number of centimeters in the length of a side of this hexagon?
Express your answer as a common fraction in simplest radical form.
With Aera A:
\(\begin{array}{|rcll|} \hline A &=& \dfrac{s^2\cdot \sin(60^{\circ})}{2} \cdot 6 \quad & | \quad \sin(60^{\circ}) = \dfrac{\sqrt{3}}{2} \\\\ &=& \dfrac{s^2\cdot \dfrac{\sqrt{3}}{2}}{2} \cdot 6 \\\\ \mathbf{A} & \mathbf{=} & \mathbf{\dfrac{3}{2} \sqrt{3}s^2 } \\ \hline \end{array}\)
\(\begin{array}{|rcll|} \hline A &=& \dfrac{s\cdot 4}{2}+ \dfrac{s\cdot 5}{2}+ \dfrac{s\cdot 6}{2}+ \dfrac{s\cdot 8}{2}+ \dfrac{s\cdot 9}{2}+ \dfrac{s\cdot 10}{2} \\\\ &=& \dfrac{1}{2}(4+5+6+8+9+10)s \\\\ &=& \dfrac{1}{2}\cdot 42s \\\\ \mathbf{A} & \mathbf{=} & \mathbf{21s} \\ \hline \end{array}\)
\(\mathbf{s =\ ?}\)
\(\begin{array}{|rcll|} \hline \mathbf{\dfrac{3}{2} \sqrt{3}s^2 } &=& \mathbf{21s} \\\\ \dfrac{3}{2} \sqrt{3}s &=& 21 \\\\ s &=& 21 \dfrac{2}{3\sqrt{3}} \\\\ s &=& \dfrac{14}{\sqrt{3}} \\\\ s &=& \dfrac{14}{\sqrt{3}}\cdot \dfrac{\sqrt{3}}{\sqrt{3}} \\\\ \mathbf{s} & \mathbf{=} & \mathbf{\dfrac{14}{3}\cdot \sqrt{3} } \\ \hline \end{array} \)
The number of centimeters in the length of a side of this hexagon is \(\mathbf{\dfrac{14}{3}\cdot \sqrt{3} } \ \text{cm}\)
