All Answers 358483 Answers

I think the answer is D. images. A transformation manipulates the shape, size, and/or direction of a shape. A few examples are rotation, dilation, and reflection.

You can double check with other people. I see why C. copies sort of makes sense, but I think the answer is still D.

- PM

I think I have the same calculator. I am not sure how to show an answer in irrational form. The calculator always converts it to decimals.

OK.....!!!

Thank you

\(3(6x+1) \equiv 4 \pmod{p}\\ 18x + 3 \equiv 4 \pmod{p}\\ 18x \equiv 1 \pmod{p}\\ 3^3 \cdot 2 x \equiv 1 \mod{p}\\ \text{It should be clear any integer }x \text{ will cause }\\ 18x \equiv 0 \pmod{2} \text{ and }18x \equiv 0 \pmod{3} \\ \text{there will be an integer solution for all other primes}\\ 2+3=5\)

\(\text{consider }g(x) = f(x) - 20\\ g(x) = a(x-5)(x-7) = a(x^2 - 12x+35)\\ \text{and for integer coefficients it's clear that }a \in \mathbb{Z}\\ g(0) = 35a\\ f(0) = g(0)+20 = 35a+20\\ |f(0)| = |35a+20|\\ \text{It should be fairly clear that }|f(0)| \text{ is minimized by }a=-1\\ \text{and thus }|f(0)|=15 \text{ is the smallest possible value}\)

There's holes in this. f isn't necessarily degree 2.  I'll need to think about it a bit to make it more rigorous.

I got 7. did I do something wrong?

Here is a computer summation of your continued fraction:
=1E100; listforeach(b,reverse(1,2,2,2.........etc ), c=b + 1/c);printc
c=1.4142135623730950488016887242097

The result is sqrt(2)

Potential Energy = k g h

                           = 80* 9.8 * 5 = 3920 j          The diver will also have KINETIC energy at this point.

x = gallons of 10%

3-x  = gallons of 40%

amount of juice in 10%  =   .1x

amount of juice in 40% =   .4(3-x)

Final amount of juice is 3 gallons at 20%    =   .2 (3)    

the ingredients = final

.1x + .4(3-x) = .2 (3)

-.3x + 1.2 = .6

-.3x = -.6

x = 2                   2 gals of 10%      3-2 = 1 gal of 40%

Since the LCM of [12, 18, 24, 30, 60] =360

Therefore the smallest positive N =360 + 6 = 366.

That IS the answer.....a balanced chemical reaction ....

   2 calciums atoms  combine with 4 water molecules to produce 2 calcium hydroxides and 2 molecules of hydrogen gas (H2)

I added the  =   because it was missing in your original question....

can i see the steps please?

Let the number of dimes = N

Then the number of nickels  = N + 6

So

number of dimes * value of each + number of nickels * value of each = total money

So  we have

N * .10  +   (N + 6) * .05   =  1.35    simplify

.10N  + 05N + .30  = 1.35

.15N + .30  = 1.35      subtract  .30 from both sides

.15N = 1.05      divide both sides by .15

N = 7    (dimes)

And the number of nickels  =  N + 6  = 7 + 6  =  13

Go CPhill! Happy B-Day! The Gods Are Focused On You!

Correct......2 hours......!!!

The probabilty is given by :

Prob 2 hits  + Prob 3 hits + Prob 4 hits

C (4,2) (.37)^2 (1 -.37)^2  + C(4,3) (.37)^3 (1 -.37) + (.37)^4 ≈ .4724  = 47.24%

Here's the image :

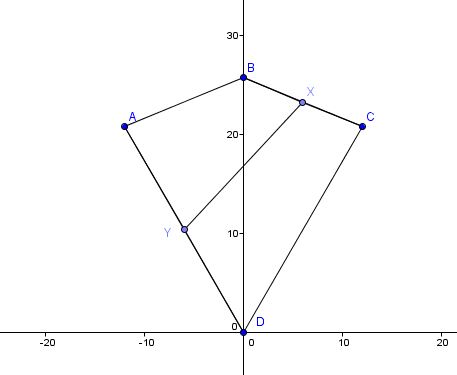
Let D = (0,0)

Let C =   ( 24sin 60, 24 sin 60) =  (12, 12sqrt3 )

And by symmetry, angle BDC  = 60/2  = 30°

We can find sin DBC as follows

sin BDC /13  =  sin BCD/24

sin30/13 = sinDBC/24

1/26 =sinDBC/24

24/26 = sin DBC

12/13 = sin DBC

So

5/13 = cos BCD

And we can find BD using the Law of Cosines

DC^2  = BD^2 + BC^2 -  2(BD*BC) cosBCD

24^2  = BD^2 +13^2  - 2(BD *13)(5/13)

576 -169  =  BD^2 - 10BD

407 = BD^2 - 10BD

BD^2 - 10BD - 407 = 0

The solution to this is

BD =  5 + 12sqrt3

So  B =   (0 , 5 + 12sqrt 3 )

So X is the midpoint of   B and D  =   

[ 12/2,  [ 5 +12sqrt(3) + 12sqrt(3)] /2  ]  =

[ 6 , 2.5 + 12sqrt(3) ]

So....by symmetry... A is  (-12, 12sqrt3) 

So....Y  is the midpoint of D and A  =  (-6, 6sqrt(3) )

So....the distance^2  X to Y  =

[ 6 - (-6) ]^2  +  [ 2.5 + 12sqrt (3) - 6sqrt(3) ]^2  =

12^2  +  [ 2.5 + 6sqrt(3) ]^2  =

144 + 6.25 + 30sqrt(3)  +108  ≈  

310.21 units

11 nickels and 5 dimes, sorry for no explanation.

I will give the answer that my calculator gives and then one of you mathematicians can break it down into smaller parts, if that is possible: 17^1507 mod 102 =17.

Yeah, I think that's what he meant.

two hours?

Since they are walking in opposite directions, we add their rates. 3+4=7mph. Now, we divide from 14 to get an answer of 2.