All Answers 357307 Answers

My Bad! I was too carred away by the LaTeX

It's an equilateral triangle.

The distance formula is $\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}.$

1. As you can use Heron's formula for the first question, we have an equilateral triangle since a=b=c=1.

The formula to find the area of an equilateral triangle is $\frac{\sqrt{3}}{4}s^2$, so we have  $\frac{\sqrt{3}}{4}1^2=\frac{\sqrt{3}}{4}\approx\boxed{0.433}.$

2. Using Heron's Formula, we have: $\sqrt{(50)(50-49)(50-33)(50-18)}=40\sqrt{17}\approx\boxed{164.92}.$

(Deleted......see CPhill's answer) 

Avg rate of change  =

[ f(b) - f(a)]

_________          let b = 8   and a  = 3       and we have

   b   -   a

[ log(4*8) + 5 ]  - [ log (4*3)  + 5 ]              log (32) -  log(12)

__________________________    =      _________________   

               8    -    3                                              5

And we can write   

log(32/12) /  5     =   log(8/3) / 5  ≈   .085

Area of rectangle = L * W

Given   :   L = 2W +1

Substitute

2W+1 * W = 28 ft^2

2W^2 +W - 28 = 0

Use Quadratic Formul to find   W =  14/4  or -4   (toss out the -4)

         L = 2W + 1 = 2(14/4) + 1 = 8

L * W  =  8 * 14/4 = 28

I believe this is correct

AB is the hypotenuse, so  AC  and AB are legs

So

BC^2  =  AB^2  - AC^2  =   area of  BCDE

BC^2  =  (AB + AC) (AB - AC)

If we let (AB - AC)  =  1......then  BC^2  will have only one prime factor, (AB + AC)

So  we have the following possibilites

AB  AC     BC   BC^2

19  18     √37     37

16  15     √31     31

15  14     √29     29

12  11     √23     23

10   9      √19    19

9     8       √17   17

7    6        √13   13

6    5        √11    11

4   3         √7      7

3   2         √5      5

2   1         √3      3

Thank you for responding, heureka.  But I still don't understand.  What do the $ actually MEAN? 

If we're just supposed to ignore them, then WHY are they there in the first place? 

I went as high as calculus in college and I've never seen this sort of terminology until I came here.

Thanks

(23, -20)   ...the x coordinate is positive, the y negative.....hence, 4th quadrant....

Area =2 x [L + W]
Width =W
Length =2W + 1
28 = 2 x [W + 2W + 1]
28 = 2 x [3W + 1]
28 = 6W + 2                 Subtract 2 from both sides
26 = 6W                       Divide both sides by 6
W = 26 / 6 = 4 1/3 - feet - the width of the rectangle
[2 * 4  1/3] + 1   = 9 2/3 - feet - the length of the rectangle. 

Often I see terms attached to $ signs in questions.  What does it mean?  I can't find any explanation on the internet.

This question is an example:  https://web2.0calc.com/questions/help-please_79935

$Math-Modus$ in LaTeX

https://web2.0calc.com/questions/help-please_79935 :

Right $\triangle ABC$ has hypotenuse $AB$. Square $BCDE$ has $BC$ as one of its sides. Suppose that the area of $BCDE$ is a prime number. If $AB$ and $AC$ are each integers less than $20$, how many possibilities are there for their lengths?

Means:

The second one has a little error.

It should use 50 not 100. 

Where did these answers come from coolstuff?

You should give credit to your source   

I'm sorry, but I'm not quite getting something. 

In the 1^st question you used s = half the perimeter

In the 2^nd question you used s = the entire perimeter  (i.e., 49+33+18=100)  

Could you clarify that for me, please?

?

Don't be so lazy.  Enter it properly.

NEVER DELETE YOUR QUESTIONS.

Someone could have been in the process of answering it!

Just write a post on the thread

         Thank people for any time they had spent answering it

         but explain that you do not need help anymore because you now have solved it yourself.

The first question has been answered here many time before. If you search it in google you will find it.

Both questions are most easlily solved with the use of probability contour maps.

Three points are selected randomly on the circumference of a circle. What is the probability that the triangle formed by these three points contains the center of the circle?

If it is a right angled triangle then the diameter will be one sides and the centre will be on this side.

If the triangle is a acute angled then the centre will be included.

If the triangle is obtuse then the centre will not be included.

I am actually going to look at the set of obtuse angled trianges which is mutually exclusive to the set of ones that include the centre.

Let the angles be x, y, and 180-(x+y)

The set of all possible triangles is contained in the region

x>0    y>0    x+y<180

Sample space area = 0.5* 180*180 units squared.

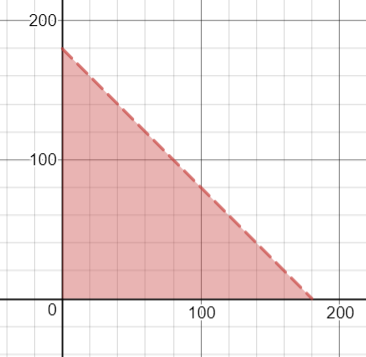
Now it will be obtuse if  x>90. or   y>90   or    x+y<90

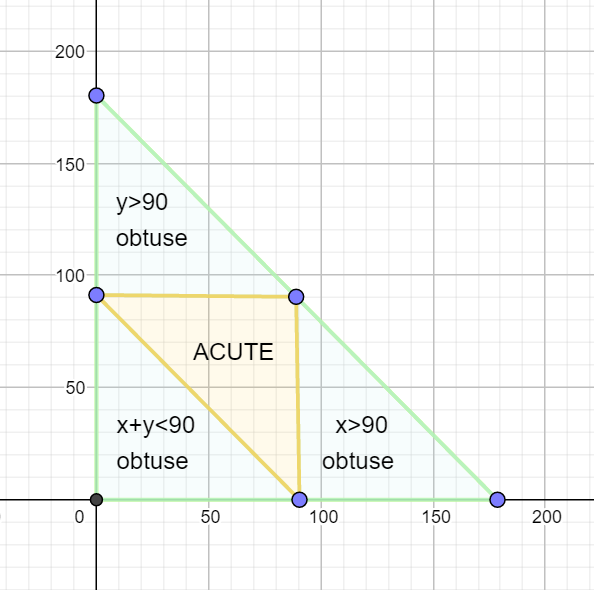
So the probability of being acute = probability of the centre being included in the triangle.

Are of included region =  0.5*90*90

$\text{P(centre included) = }\frac{0.5*90*90}{0.5*180*180}=\frac{1}{4}$

how do you work out...
4^5 divided by 4^2
(without a calculator)
so, on a test paper when you do not have a calculator

3.

$\begin{array}{|rcll|} \hline && \dfrac{4^5}{4^2} \\\\ &=& 4^{5-2} \\ &=& 4^3 \\ &=& 4*4*4 \\ &=& 16*4 \\ &=& 64 \\ \hline \end{array}$

how do you work out...
4^5 divided by 4^2
(without a calculator)
so, on a test paper when you do not have a calculator

2.

$\begin{array}{|rcll|} \hline && \dfrac{4^5}{4^2} \\\\ &=& \dfrac{4^34^2}{4^2} \\\\ &=& 4^3 \\ &=& 4*4*4 \\ &=& 16*4 \\ &=& 64 \\ \hline \end{array}$

how do you work out...

4^5 divided by 4^2

(without a calculator)

so, on a test paper when you do not have a calculator 

1.

$\begin{array}{|rcll|} \hline && \dfrac{4^5}{4^2} \\\\ &=& \dfrac{4*4*4*4*4}{4*4} \\\\ &=& 4*4*4 \\ &=& 16*4 \\ &=& 64 \\ \hline \end{array}$

What is the largest positive integer n such that 1457 and 368 leave the same remainder when divided by n?

What is the largest positive integer n such that 1457, 368, and 1754 all leave the same remainder when divided by n?

Let the roots of

$z^3 = 2 + 2i$

be $a_1 + ib_1$, $a_2 + ib_2$ and $a_3 + ib_3$.
Compute $a_1 a_2 a_3$.

$\begin{array}{|rcll|} \hline \mathbf{z^3} &\mathbf{=}& \mathbf{2 + 2i},\ \quad z^3=a+ib \\\\ && \text{convert 2+2i to polar form:}\\ && r = \sqrt{a^2+b^2} = \sqrt{2^2+2^2} = \sqrt{8}= \sqrt{2^3} \\ && \sqrt[3]{r} = \sqrt[3]{\sqrt{2^3} } = \sqrt[3]{ 2^\frac{3}{2} } = \left( 2^\frac{3}{2} \right)^{\frac{1}{3} } = 2^\frac{1}{2} = \sqrt{2} \\ && \theta = \arctan\left(\dfrac{b}{a}\right) = \arctan\left(\dfrac{2}{2}\right) = \dfrac{\pi}{4} \\ && \theta_i = \dfrac{\dfrac{\pi}{4}+2\pi k} {3} \\ && \theta_i = \dfrac{\pi}{12} + \dfrac{2}{3} \pi k ,\quad k= 0,\ 1, 2 \\\\ && \theta_1 = \dfrac{1}{12} \pi,\quad \theta_2 = \dfrac{3}{4} \pi, \quad \theta_3 = \dfrac{17}{12} \pi \\ \hline \end{array}$

$\begin{array}{|rcll|} \hline z_0 &=& \sqrt{2} \left( \cos\left( \dfrac{1}{12} \pi\right) +i\sin\left(\dfrac{1}{12} \pi \right)\right) \quad | \quad \cos\left( \dfrac{1}{12} \pi\right) = \dfrac{\sqrt{2}(\sqrt{3}+1) }{4} \\ z_1 &=& \sqrt{2} \left( \cos\left( \dfrac{3}{4} \pi\right) +i\sin\left(\dfrac{3}{4} \pi \right)\right) \quad | \quad \cos\left( \dfrac{3}{4} \pi\right) = -\dfrac{\sqrt{2}}{2} \\ z_2 &=& \sqrt{2} \left( \cos\left( \dfrac{17}{12} \pi\right) +i\sin\left(\dfrac{17}{12} \pi \right)\right) \quad | \quad \cos\left( \dfrac{17}{12} \pi\right) = -\dfrac{\sqrt{2}(\sqrt{3}-1) }{4} \\ \hline \end{array}$

$\begin{array}{|rcll|} \hline \mathbf{a_1 a_2 a_3} &=& \sqrt{2} \dfrac{\sqrt{2}(\sqrt{3}+1) }{4} \sqrt{2}\left(-\dfrac{\sqrt{2}}{2}\right) \sqrt{2}\left(-\dfrac{ \sqrt{2}(\sqrt{3}-1) }{4} \right) \\ &=& \dfrac{1}{4} (\sqrt{3}+1)(\sqrt{3}-1) \\\\ &=& \dfrac{3-1}{4} \\\\ &=& \dfrac{2}{4} \\\\ &\mathbf{=}& \mathbf{\dfrac{1}{2}} \\ \hline \end{array}$