All Answers 353025 Answers

+997

+8

STEP 1.

So, we have a right triangle $\triangle {ABC}$ with $\angle B = 90^\circ$.

Let sides ${AC} = a$, $AB = b$. and $CB = c$.

$2\sin A$ is equal to $2(\frac{c}{a})$, and $3\cos A $ is equal to $3(\frac{b}{a})$

Therfore,

$2(\frac{c}{a}) = 3(\frac{b}{a})$,

$\frac{2c}{a} = \frac{3b}{a}$,

$2c = 3b$.

STEP 2.

$\tan A$ is equal to $\frac{c}{b}$.

We can substitute $c$ for $\frac{3b}{2}$.

$\tan A$ $=$ $\frac{\frac{3b}{2}}{b}$,

$\tan A$ $=$ $\frac{3b}{2} \times \frac{1}{b}$,

$\tan A$ $=$ $\boxed{\frac{3}{2}}$

.

KnockOutJun 28, 2019

+6248

+1

$\text{quadratic formula}\\ x = \dfrac{2\pm \sqrt{(-2)^2-(4)(1)(2)}}{2(1)} = \dfrac{2\pm \sqrt{-4}}{2} = 1 \pm i$

.

RomJun 28, 2019

+936

+2

Ummmmmmmmmmmmmmmmmmmm...

This was a question on a 40 minute test with 30 questions, and I'm not exactly sure this would work in that time. But I really think you spent a lot of effort doing that and that's really great.

dgfgrafgdfge111Jun 28, 2019

#5

+434

0

Yes, I understand how to do a varibles inverse I didn't realize for fractions it's considered adding on varibles in the this situation. thanks!

HiylinLinkJun 28, 2019

#4

+3

Also, x didn’t vanish like you mentioned, it was originally -1/2x it is now positive 1/2x

GuestJun 28, 2019

+1

If you want to simply “move” the x over, you need to reverse the sign

for example

x+3=2x

x-2x+3=0

-x+3=0

and to move 3 over,

-x=-3

then mutiply by -1

x=3

GuestJun 28, 2019

+434

0

Thanks alot for your effort : ) but the one part I'm having trouble grasping is when you add x to both side's do you mean are you carrying x from the rigth side of the equation over to the left? and if so what were the effects exactly because x seemed to have vanished formt he problem entrily leaving only the x that is being multiplied by the 1/2 in it's original state...

Wait sorry XD for that incovience I see now 1/2 times x becomes positive when you carry over the x formt he left side THANKS ALOT and have a great day!

HiylinLinkJun 28, 2019

+2

Right now, you are given -1/2x+3=-x+7

add x on both sides

1/2x+3=7

Subtract 3 on both sides

1/2x=4

mutiply by 2

x=8

GuestJun 28, 2019

+33616

0

This question was asked and answered here: https://web2.0calc.com/questions/help_84836#r5

AlanJun 28, 2019

+36916

0

Here is one way:

tanr = sinr /cos r = 5 cos q

sin r = cos r 5 cos q

pq/15 = pr/15 5 pq/15

1 = 5 pr/15

3 = pr use pythag theorem to find pq = sqrt 216

ElectricPavlovJun 28, 2019

+36916

0

cos a = cos 90 = 0

ElectricPavlovJun 28, 2019

#4

0

With guesswork you might just get lucky, as with this example.

The problem is that you are not told that the numbers are integers, you're simply told that they are real numbers.

It could happen that none of your guesses work.

GuestJun 28, 2019

Source: https://www.careerbless.com/aptitude/qa/permutations_combinations_imp7.php#p1

+26367

+1

B:
How many ways are there to put 5 balls in 3 boxes if the balls are distinguishable but the boxes are not?

I assume:
$\text{ Let $k=5$ distinct balls } \\ \text{ Let $n=3$ identical boxes } $

Formula:
$\begin{array}{|rcll|} \hline \text{Distribution of $k$ distinct Balls into $n$ identical Boxes} =\sum \limits_{i=1}^{n}S(k,i) \\ \text{$S(k,n)$, Stirling number of the second kind } \\ \hline \end{array} $

$S(k,n)$:

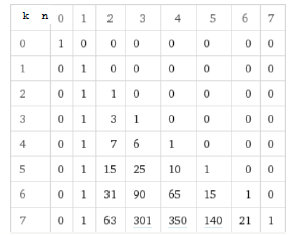
Source: https://www.wolframalpha.com/input/?i=stirling+number+second+kind

$\begin{array}{|rcll|} \hline \text{Distribution of $5$ distinct Balls into $3$ identical Boxes} &=&\sum \limits_{i=1}^{3}S(5,i) \\ &=& S(5,1)+ S(5,2)+S(5,3) \\ &=& 1 + 15 + 25 \\ &=& 41 \\ \hline \end{array} $

heurekaJun 28, 2019

see: https://web2.0calc.com/questions/help_26367#r5

+26367

+1

A:

Mack the bug starts at $(0,0)$ at noon and each minute moves one unit right or one unit up. He is trying to get to the point $(5,7)$.

However, at $(2,3)$ there is a spider that will eat him if he goes through that point. In how many ways can Mack reach $(5,7)$?

or see: https://web2.0calc.com/questions/help_26367#r6

heurekaJun 28, 2019

+33616

+3

Here's a systematic way of approaching this:

AlanJun 28, 2019

+1

Formula: Sum of ODD consecutive numbers =n^2, whre n =number of terms.

Number of terms =[2019 - 1] / 2 + 1 =1010 terms.

n^2 =1010^2 =1,020,100 - sum of consecutine ODD numbers.

Formula: Sum of consecutive EVEN numbers =n x (n + 1), where n = numbers of terms.

Number of terms =[2018 - 2] / 2 + 1 =1009 terms.

n*(n +1) =1009 * 1010 =1,019,090 - sum of consecutive EVEN numbers

Difference =sum of ODD numbers - sum of EVEN numbers =1,020,100 -1,019,090 =1010

GuestJun 28, 2019

-1

0

arcsin (- .73 ) = -46.89 degrees ( or 313.11 degrees) and 226.89 degrees

roll the ball

jimrookerJun 28, 2019

+26367

+2

2)
Let $a,b,c$ be positive real numbers such that $\log_a b + \log_b c + \log_c a = 0$.
Find $(\log_a b)^3 + (\log_b c)^3 + (\log_c a)^3$.

$\text{Let $\log_a b = \mathbf{x} $} \\ \text{Let $\log_b c = \mathbf{y} $} \\ \text{Let $\log_c a = \mathbf{z} $} $

$\begin{array}{|rcll|} \hline \log_a b + \log_b c + \log_c a &=& 0 \\ \mathbf{x+y+z} &=& \mathbf{0} \qquad (1) \\ \hline \end{array}$

$\begin{array}{|rclrcl|} \hline \log_a b &=&\dfrac{\log_c b}{\log_c a} \quad&| \quad \log_c b &=&\dfrac{\log_b b}{\log_b c} \\\\ \log_a b &=&\dfrac{\log_b b}{\log_b c\log_c a} \quad&| \quad \log_b b = 1 \\\\ \log_a b &=&\dfrac{1}{\log_b c\log_c a} \\\\ \log_a b\log_b c\log_c a &=& 1 \\\\ \mathbf{xyz} &=& \mathbf{1} \qquad (2) \\ \hline \end{array}$

$\begin{array}{|rcll|} \hline (x+y+z)^3 &=& (x+y+z)^2(x+y+z) \\ &=& \left(x^2+y^2+z^2+2(xy+yz+xz)\right)(x+y+z) \\ &=& (x^2+y^2+z^2)(x+y+z)+ 2(x+y+z)(xy+yz+xz) \\\\ &=& x^3+y^3+z^3 \\ && +x^2y+x^2z+y^2x+y^2z+z^2x+z^2y + 2(x+y+z)(xy+yz+xz) \\\\ &=& x^3+y^3+z^3 \\ && +(x+y+z)(xy+yz+xz) -3xyz + 2(x+y+z)(xy+yz+xz) \\\\ (x+y+z)^3&=& x^3+y^3+z^3 -3xyz + 3(x+y+z)(xy+yz+xz) \\ \hline \mathbf{x^3+y^3+z^3} &=& \mathbf{(x+y+z)^3-3(x+y+z)(xy+yz+xz)+3xyz} \qquad (3) \\ \hline \end{array}$

$\begin{array}{|rcll|} \hline \mathbf{x^3+y^3+z^3} &=& \mathbf{(x+y+z)^3-3(x+y+z)(xy+yz+xz)+3xyz} \\ && \boxed{x+y+z = 0} \\ x^3+y^3+z^3 &=& 0^3-3\cdot 0\cdot (xy+yz+xz)+3xyz \\ x^3+y^3+z^3 &=& 3xyz \\ && \boxed{xyz = 1} \\ x^3+y^3+z^3 &=& 3\cdot 1 \\ x^3+y^3+z^3 &=& 3 \\ \mathbf{(\log_a b)^3 + (\log_b c)^3 + (\log_c a)^3} &=& \mathbf{3} \\ \hline \end{array}$

heurekaJun 28, 2019