All Answers 358162 Answers

The ratio  of the  side  lengths  is  just   sqrt (63)  / sqrt (35)  =

sqrt  (9 * 7)   /sqrt  ( 5 * 7)   =

3 sqrt ( 7)  / [ sqrt (5) * sqrt (7) ]  -

3 / sqrt (5)    =

3sqrt (5)  / 5

a + b + c  =   

3 + 5  +  5   =

13

5.8pi * 10.5 = 60.9pi

So the area of the plastic lable is 60.9pi. 

I hope this helped. :)))

=^._.^=

thank you

1/9*|5a + 2| < 1

|5a + 2| < 9

-9 < 5a + 2 < 9

-11 < 5a < 7

-11/5 < a < 7/5

a = (-11/5, 7/5)

I hope this helped. :)))

=^._.^=

52 *  5 =   260

260  =  _____  *  (10/2)

260  =   ______ *   5

260  / 5  =    52   

52 x 5 = 260

52 * 10  / 2 = 260

No solution....to see why....note that we  have

6x +  12 =  6x +  2            subtract  6x from both sides

12  =  2              absurd.....so......no solution possible

You're right, I forgot about -12

Here's a simple explanation for a specific value of n that might help before you try to understand a more general proof.

This is equivalent  to  finding  out  how many identifiable sequences can be  made  from  1,2,2,3,3,3

This is given  by

              Number  of  values !

_______________________________________       =  

(Repeated values of 2) ! (Repeated values of 3)! 

 6!                   720              720

_____   =      _____  =     _____  =      60   identifiable  sequences

2! 3!                2 * 6             12

Obtuse isosceles triangle

1. 1/3 x 1/3 = 1/9

2. 2/3 x 4/1 = 8/3 = 2 2/3

Very astute, textot   !!!!

f(x)  =  2    means  that  y   = 2

Only two points on this graph intersect  this line  .....   (1,2)  and  ( 2.5, 2)

So...the sum of the x coordinates  =    1 + 2.5 =   3.5

I suspect question 1 is meant to look like the following (also integration by parts):

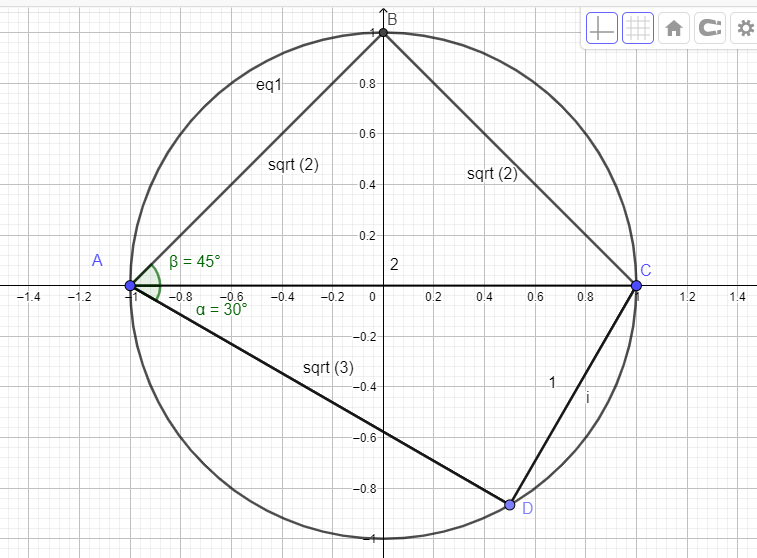
We  can  choose any  convenient  value  for  the  diameter.....let  this  =  2...so  the radius = 1

Angles  ADC  and  ABC  will be right angles

So   in right  triangle ADC  angle  DAC = 30°   and angle  DCA   = 60°

So  DC  =  1       AD  =  sqrt (3)

So area of  triangle ADC  = (1/2) (1) (sqrt (3)   = sqrt (3)/2

And  triangle  ABD  will  be isosceles  right  with  AB  = BC  =  2/sqrt (2)   = sqrt (2)

So  the area of  triangle   ABD  =   (1/2) [sqrt (2)]^2   =  1

So   [ ABCD ]   =  1 + sqrt (3) / 2     =  [ 2 + sqrt (3) ]  /2

And the area of the  circle  =  pi 1^2  =  pi

So     [ABCD ]   / area of  circle  =       (2 + sqrt (3) )  /  ( 2 *  pi )  =   (2 + sqrt (3)  / (2pi)

So   a +  b +  c  =  2 + 3 + 2   =   7

Here's a pic :

question 3

let 

\(u=x \qquad and \qquad v'=g''(x)\)

And again use integration by parts

Question 1: 

I do not understand the question. 

Please just put one question per post.

Question 2

let     

 \(u=2x^2   \quad and  \quad v'=2xe^{x^2}\)

Now  use integration by parts to solve.    

Come back here with your answer.

2/3    ÷  4     =

2/3  ÷  4/1         

Rule  for  dividing  fractions  :

"keep the first fraction  -   change  to  multiplication   -   flip the second  fraction  "

2/3  *   1/4    =       2/ 12   =   1/6   of a  gallon in each bottle

We have  two equations  here

t/3  - 5  <  t   - 2                            t  - 2  ≤   -3t + 7 

-5 + 2  <  t   -t/3                            t + 3t  ≤  7 + 2

-3  <  (2/3)t                                      4t ≤  9

-3(3/2) <  t                                          t ≤ 9/4

-9/2  < t

-9/2  < t  ≤ 9/4

The midpoint of AB   will  be  C  = [ ( 24  -3)/2  , (7 + 4)  /2  ]  =  (21/2 , 11/2)  

So

2(21/2)   - 4(11/2)  =

21  - 22   = 

-1 

Let A  = (0,0)

B  =  (2,0)

E  =(1,1)

BE    =  the radius of the  circle  =   sqrt  [ (2-1)^2  +(1-0)^2  ] = sqrt (2)

F =  (2 -sqrt (2)  ,  0)

EF  =  sqrt   [ ( 2 - sqrt (2)  - 1)^2  + 1^2  ]  =   sqrt  [ ( 1  -sqrt (2))^2  + 1  ) ]  = 

sqrt [ 1 - 2sqrt (2) + 2  + 1]  =  sqrt  (4  -2sqrt (2) )  =  sqrt [ 4  -sqrt (8) ] 

Using the  Law of  Cosines

EF^2   = BE^2 + BF^2  - 2 ( BE * BF)  cos EBF

4 -sqrt (8)  =  2  + 2  -  2(2) cos EBF

-sqrt (8)  =   -4 cos EBF

sqrt (8)  / 4 = cos EBF

2sqrt ( 2)   /4  =cos  EBF

sqrt (2)   / 2 = cos EBF

So EBF  = 45°

Area of  the  circle  =  pi  (sqrt (2))^2  ( 1/8)   =  pi/4

Area of shaded  region  =  area of  rectangle  -area of  circle  =

AB * BC  -  pi/4  =

2 * 1    -  pi/4   =

2  - pi/ 4   =

(1/4) ( 8  - pi)

a =  4     b  =   8

And their  sum  =  12

(2x + 7) ( x  - 5)  =  -43  +  jx

2x^2  + 7x  - 10x  - 35   = -43  + jx

2x^2 - 3x - 35  =  -43 + jx

2x^2  - (3 + j)x  +  8  = 0

If this has a  single real solution , the  discriminant =    0 

So

(3 + j)^2   - 4(2)(8)    =  0

j^2  + 6j +  9   - 64  = 0

j^2  + 6j   - 55   =   0         factor

(j - 5)  ( j + 11)     =   0

Settng each factor to 0  and  solving  for   j gives us

j  -  5   =  0                       j + 11    =   0

j =  5                                 j  =  -11