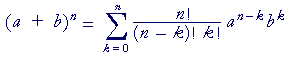All Answers 359399 Answers

see my " all the best " works ! alan came so fast for ur helt after my " all the best " isnt it ! 

Hi Heureka,

Mine is not wrong.

nCr is always identical to in value to nC(n-r)

10C4=10C6   

your answer and my answer are identical.

Here's how it's done for your simple example.  It isn't always possible to get nice results for situations where a(t) and b(t) are very complicated.  For those, use a numerical method!

I need to correct one item above.  In general the integrating factor is $$e^{\int{-a(t)}dt}$$  not $$e^{-a(t)t}$$.

Just noticed Bertie has said this below.

okay , the name sounds a bit scary but ill try to find out ! all the best for ur search !

Sure,

they are called non-autonomous linear first order differential equations.

is there a name of these kind of questions ? 

Thank you Heureka 

$$\mbox{simplify } (12c+9b)-(6c-7b)$$

(12c+9b)-(6c)-(-7b)

(12c+9b)-(6c)+(7b)

(12c)+(9b)-(6c)+(7b)

(12c)-(6c)+(9b)+(7b)

(12c-6c)+(9b+7b)  

(12-6)c+(9+7)b

(6c)+(16b)

$$\boxed{6c+16b}$$

The derivate of  $$y=\dfrac{t}{\sqrt{(ct^2-1)}} = t*\left( ct^2-1\right)^{-\frac{1}{2}}$$

Product Rule: $$y^\prime=t * \left( \frac{d(ct^2-1)^{-\frac{1}{2}}}{dt} \right)+\frac{d(t)}{dt}*(ct^2-1)^{-\frac{1}{2}}$$

$$y^\prime=t *(-\frac{1}{\not{2}})(ct^2-1)^{-\frac{1}{2}-1}}*\not{2}ct + 1*(ct^2-1)^{-\frac{1}{2}}$$

$$y^\prime=-ct^2(ct^2-1)^{-\frac{3}{2}}} + (ct^2-1)^{-\frac{1}{2}}$$

$$y^\prime=\dfrac{1}{\sqrt{(ct^2-1)}} -\dfrac{ct^2}{
\left(
\sqrt{(ct^2-1)}
\right)^3
}$$

$$\boxed{y^\prime=\dfrac{1}{\sqrt{(ct^2-1)}}
\left(
1-\dfrac{ct^2}{ct^2-1}
\right)}$$

$$\\y=\dfrac{1}{4}*\cos^{-1}(2x)\\
\mbox{Now change y and x }\quad
\textcolor[rgb]{1,0,0}{x}=\dfrac{1}{4}*\cos^{-1}(2\textcolor[rgb]{1,0,0}{y})\\
4x=\cos^{-1}(2y)\quad | \quad \cos\\$$

$$\\\cos{(4x)}= 2y\\
2y = \cos{(4x)} \quad | \quad :2\\
\boxed{y=\dfrac{1}{2}*\cos{(4x)}} \quad inverse$$

Math(Input=Result) Error!

$${binom}{\left({\left({\frac{{\mathtt{3}}}{{{\mathtt{x}}}^{{\mathtt{2}}}}}{\mathtt{\,-\,}}{\mathtt{4}}{\mathtt{\,\times\,}}{{\mathtt{x}}}^{{\mathtt{3}}}\right)}^{{\mathtt{10}}}\right)} = {binom}{\left(\tiny\text{Error: loop}\right)}$$

$$\left(\dfrac{3}{x^2}-4x^3\right)^{10}\\$$

I think the answer is:

$$10Cr\times \left(\dfrac{3}{x^2}\right)^{\textcolor[rgb]{1,0,0}{10-r}}\times (-4x^3)^{\textcolor[rgb]{1,0,0}{r}}\\
=10Cr\times 3^{10-r} \times (-4)^r \times x^{-2(10-r)} \times x^{3r}\\
=10Cr\times 3^{10-r} \times (-4)^r \times x^{-2(10-r)+3r}\\
=10Cr\times 3^{10-r} \times (-4)^r \times x^{-20+2r+3r}\\
=10Cr\times 3^{10-r} \times (-4)^r \times x^{-20+5r}$$

so -20+5r=0  -> r = 4

the term we want is

$$10C\textcolor[rgb]{1,0,0}{4}\times 3^6\times (-4)^4 \times x^0$$

I assume that by "equivalent equation" you mean rearrange to get t = ...

Take log to the base 2 of both sides

log₂y = log₂(2.5*2^t/5)

log₂y = log₂(2.5) + log₂(2^t/5)

log₂y = log₂(2.5) + t/5

t/5 = log₂y - log₂(2.5)

t/5 = log₂(y/2.5)

t = 5log₂(y/2.5)

 5 = f(-3)   ...(1)

 9 = f(8-h)+k   ...(2)

Subtract 4 from both sides of (2)

5 = f(8-h) + k-4   ...(3)

Comparing (1) and (3) it looks like h is 11 and k is 4.

(5, 12) on y = g(x) means 12 = g(5)    ...(1)

(n, 19) on y = g(9x-6)+7 means  19 = g(9n-6)+7   ...(2)

Subtract 7 from both sides of (2) to get 12 = g(9n-6)   ...(3)

Compare (1) and (3).  Clearly 5 = 9n - 6, so n = 11/9

Where 2-secx = 0

So secx = 2  or  cosx = (1/2)

So we have (pi/3 + 2n*pi)   and (5/3)pi + 2n*pi).....where n is an integer

Rs 51

cos^2 x-sinx-sin^2 x=0      writing cos^2x as 1 - sin^2x, we have

1-sin^x - sinx - sin^2x = 0

-2sin^x - sinx + 1  =  0        ....multiply through by -1

2sin^x + sinx - 1 = 0            .....factor

(2sinx - 1) (sinx + 1) = 0      ....set each factor to 0

2sinx - 1 = 0            sinx + 1 - 0

sinx = 1/2                sinx = -1

x = 30° , 150°  and 270°

So....x = 30°

so what is the first instalment?

Great job, NinjaDevo......well presented, too...Thumbs Up and Points......!!!!

2log₄(16xy²)

2 [ log₄16 + log₄x + log₄y² ]

2 [ 2 + log₄x + 2log₄y ]

4 + 2log₄x + 4log₄y

And that's in "linear" form..... (no exponents)

Excellent as always Kitty.

You go to the swagmaster and preform some supe swaggy swagalicious swag-tasks.

actually that x came from my confusing head , u know ive recently got the habbit of thinking the right answer and then thinking some more and writing the wrong one! the answer u got is the same one i got ! by the way thanks for the right way ! thumbs up,!