All Answers 356736 Answers

the center of the circle =  (-1, 1)

the radius of the circle  =  \(\sqrt{(-1-1)^2+(1-2)^2}\,=\,\sqrt{(-2)^2+(-1)^2}\,=\,\sqrt{4+1}\,=\,\sqrt5\)

So the equation of the circle is...

\((x--1)^2+(y-1)^2\,=\,\sqrt5^2 \\~\\ (x+1)^2+(y-1)^2\,=\,5 \\~\\ (x+1)(x+1)+(y-1)(y-1)\,=\,5 \\~\\ x^2+2x+1+y^2-2y+1\,=\,5 \\~\\ x^2+2x+y^2-2y+2\,=\,5 \\~\\ x^2+2x+y^2-2y-3\,=\,0 \\~\\ x^2+y^2+2x-2y-3\,=\,0 \)

A + B + C + D   =   1 + 2 - 2 - 3   =   -2

Here's a graph to check the equation of the circle:

3.

a)   

 In the form  ( x - h)^2  + (y - k)^2  = r^2    .... we can write this as

(x - 0)^2 + ( x -  (-5) )^2   = 9

The center  is  ( h , k)  =  ( 0 , -5)    ....so Jenna is incorrect

b)   9  =  r^2  ...so   the radius is the square root of this     = 3 units

So....the diameter is twice this  =  6 units

Raul is incorrect, as well  !!!

We need to find the radius...

The surface area is given by :      4 pi * r^2

So

16 pi  =  4 pi * r^2     divide both sides by pi

16  = 4r^2     divide both sides by 4

4  = r^2       take the positive root

2  ft  = r

So...the volume of a sphere is

(4/3) pi ( radius)^3  =

(4/3) pi (2) ^3

(4/3) pi * 8

(32/3) pi   ft^3   ≈   10.66 pi  ft^3

None of the given answers are correct  !!!

Thank you

1.  Once we fold the sides up....the dimensions of the  base will be

(8 - 2x) (10 - 2x)

And the height will be x

So....the volume, V, is   area of the base * height  =

a)  V = (8 - 2x) (10 - 2x) x

b)  Here's a graph   of the function :

https://www.desmos.com/calculator/ubq8tavuol

The value of x that gives the max volume is when we look at the top of the curve between x  = 0  and x = 4....this value is :   x  ≈ 1.5  in

Hi EP,

I appologise EP your answers are correct.  

You probably do not need to worry about this explaination, I expect you already know it.

It might hlp the guest that asked though.

What I was getting at is this  (but it makes no differnence for this question)

The definition of a function is that for every x vlaue there can be at most 1 y value.

If it is graphed this is easy to see from the straight line test.

The inverse of a funtion is its reflection in the line y=x

When you do this, most times the reflection is NOT a function, so you need to be very careful about the new domain.

All the teachers I have ever discussed this with say you must rearrange the equation to make x the subject BEFORE you swap the x with the y BECAUSE then the new domain and range are more easily seen.

I cannot see why they make this demand so strongy but certainly people must be extremely careful about constraints.

say if

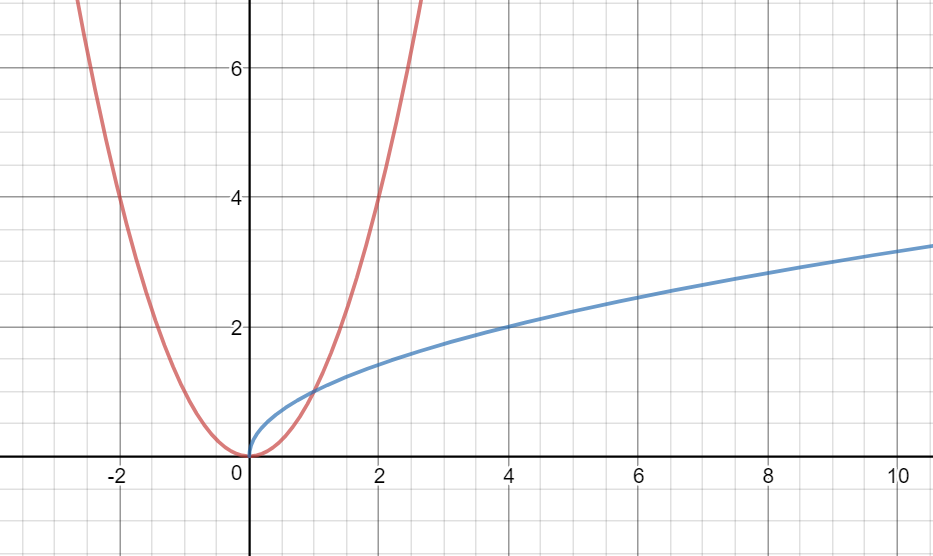
y=x^2  this is a normal concave up parabola

If you just swap the lpronumerals like you said then you get   x=y^2    This is a sideways parabola BUT it is not the inverse function of y=x^2 because it is NOT a function at all.

To find the inverse of y=x^2 you should rearange the formula first and make sure that for each y value there is ONLY one x.

THEN you can swap the letters over.

\(y=x^2\\ \pm\sqrt{y}=x\\ x=\pm\sqrt{y}\\ \text{It can easily be seen that } y\ge0\\ \text{Swap pronumerals and drop the minus sign}\\ y=\sqrt x \qquad \text{If you include both answers this will not be a function }\\ \text{The inverse of }y=x^2 \text{ is } y=\sqrt{x} \quad x\ge 0 ,\quad y\ge0 \)

Here is the graph of y=x^2 in red and its inverse function in blue

2. 

a) The volume of the aquarium is  s^3  =  3^3  =   27 ft^3

The weight will be    27 * 62  = 1674 lbs.     the table will NOT support that !!!

b)  The density of water is the same, no matter the volume

Sorry, cerenetie......no clue  !!!

2.What is the area of the region defined by the equation $x^2+y^2 - 7 = 4y-14x+3$?

Rewrite  as

x^2 + 14x +y^2 - 4y = 10

This is a circle....we need to complete the square on x and y  [ I'm assuming that you are familiar with this?? ]

x^2 + 14x + 49  + y^2 - 4y + 4  =  10 + 49 + 4

The right side simplifies to  63  = ( radius of the circle)^2

So... the area  is    pi * r^2   =  pi *63  ≈  197.9  units^2

I have 2 question

1.The graph of the quadratic $y = ax^2 + bx + c$ has the following properties: (1) The maximum value of $y = ax^2 + bx + c$ is 5, which occurs at $x = 3$. (2) The graph passes through the point $(0,-13)$. If the graph passes through the point $(4,m)$, then what is the value of $m$?

2.What is the area of the region defined by the equation $x^2+y^2 - 7 = 4y-14x+3$?

1. The vertex  (3, 5)  and the point  (0, - 13)  are on the graph ....and  (3,5)  is tthe vertex

The x coordinate of the vertex is given by :

-b / [2a]  =  3

-b = 6a

b = - 6a

And  since  (0, - 13)  is on the graph, then  c  =  -13

And using the vertex, we can find "a"  thusly

5  =  a(3)^2  - 6a(3)   - 13

18  = 9a- 18a

18  =  -9a

-2  = a       ⇒   b  = -6(-2)  =  12

So...our function is

y   =  -2x^2 + 12x - 13

And when x  =  4, m  =

-2(4)^2  + 12(4)  - 13

-32 + 48  - 13

3

So....the point (4,3)  is on the graph

Here's a graph : https://www.desmos.com/calculator/jhmml2xcki

Solve for x:

(log(x^2))/log(2) - log(x)/log(2) = 5

Rewrite the left hand side by combining fractions. (log(x^2))/log(2) - log(x)/log(2) = (log(x^2) - log(x))/log(2):

(log(x^2) - log(x))/log(2) = 5

Multiply both sides by log(2):

log(x^2) - log(x) = 5 log(2)

log(x^2) - log(x) = log(1/x) + log(x^2) = log(x^2/x) = log(x):

log(x) = 5 log(2)

5 log(2) = log(2^5) = log(32):

log(x) = log(32)

Cancel logarithms by taking exp of both sides:

x = 32

First one

The function is continuous  until x  = 0.......we have a discontinuity where the function's y value approaches  1  from the left side ...then, the  point (0,0) is on the graph....and then we have another discontinuity where the function approaches -1 from the right at x  = 0....from here, the function is continuous to infinity

Here's a graph  : https://www.desmos.com/calculator/gliwclwbrn

Second one

This is easier......we have the line  y  = x + 1....it is defined at all x values except at x  = 2...where  the point  (2, 1) appears on the graph.....thus, the first function approaches 3 from the left and right as x approaches 2 but it discontinous at x  = 2

Here's the graph : https://www.desmos.com/calculator/x3b14cad9o

log₂ x^2 + log _1/2 x   =  5

2 log₂ x + log _1/2 x  =  5            use the change-of-base rule to write

2 [ log x / log 2]  +  log x / log (1/2)  =  5        { log (1/2)  =  log 2^(-1) }

2[log x ] / log 2 ] + log x / log 2^(-1) =  5

2[;og x / log 2 ] +  log x / -log 2  = 5

2 [ log x / log 2 ]  - logx/ log 2  = 5

[2logx - log x ] / log 2  = 5

log x/ log 2  = 5

log x  =  5log 2

log x  =  log 2^5

log x  = log 32

x  = 32

Note....cos (-theta)  = cos (theta)

sin (theta)  =  - sqrt ( 1^2  - (sqrt (3)/4)^2 )   =  -sqrt ( 1 - 3/16)  = -sqrt (13) /4  

Thank you!!

Thanks so much!

I believe it will be a common well known right triangle   3 -4 -5

you basically have two areas 3 x 4      (because two triangles add to a 3 x 4 rectangle)

3x4 x 2 = area

Cool?

sin²θ  +  cos²θ   =   1

(1/4)²  +  cos²θ   =   1

cos²θ   =   1  -  (1/4)²

cos²θ   =   1  -  1/16

cos²θ   =   15/16

cos θ   =   ±√[ 15/16 ]

cos θ   =   ±√15 / 4

Since  sin θ  is positive and  tan θ  is positive,  cos θ must be positive.

cos θ   =   √15 / 4

sin²θ  +  cos²θ   =   1

sin²θ  +  (3/5)²   =   1

sin²θ   =   1  -  (3/5)²

sin²θ   =   1  -  9/25

sin²θ   =   16/25

sin θ   =   ±√[ 16/25 ]

sin θ   =   ± 4 / 5

Since  θ  is in Quadrant I,  sin θ  is positive.

sin θ   =   4 / 5

tan θ   =   sin θ / cos θ

tan θ   =   ( 4/5 ) / (3/5 )

tan θ   =   4 / 3

Hi G

I remember when I first had problems with inverse functions and there are many out there that still do so dont feel too bad as it is be a difficult topic to master. Hope it helps, what I did was firstly read over the definition a number of times until it made sense to me then I went over some really simple examples and drew graphs of each situation to further help things sink in...basically like many mathematical concepts you need to devote a lot of time and effort and oftem frustration until it sinks in and then when finally the penny drops and it will you will wonder why it took so long because it now seems so easy. One piece of information which helped is to know that inverse functions as graphs are reflections of one another in the line y=x as you can see in the graph given by EP. Lets look at a reasonably simple example. Find the inverse function of y=x². Oh by the way another gem...it needs to be a function as the name implies....Really what all the fuss is about who knows as all you are doing is swapping the x values with the y values for each point in question ie

          if y = x²  then the inverse is x = y² and so we use algebra to rearrange this to make y the subject ie y=sqr(x) or

y=-sqr(x). Now if you sketch these two functions you get your standard parabola and the same parabola rotated through 90^° to the right. Now draw the line y=x. you will see that y=x² and x=y² are reflections in y=x. However, x=y²is not a function but y=sqr(x) ie positive root is. So the inverse function of y=x² is by definition the positive root y=sqr(x) and the fact that y=x² has a range of y>=0 which becomes the domain of the inverse ie y=sqr(x),x>=0.

Also look for points of intersection to help find the inverrse function.

Hope this was a bit of a help. Remember the key is practice practice practice!!!

sin²θ  +  cos²θ   =   1

(3/4)²  +  cos²θ   =   1

cos²θ   =   1 - (3/4)²

cos²θ   =   1 - 9/16

cos²θ   =   7/16

cos θ   =   ±√[ 7/16 ]

cos θ   =   ±√7 / 4

Since  θ  is in Quadrant II , cos θ is negative.

cos θ   =   - √7 / 4

Since   \(1-\cos^2\theta=\sin^2\theta\)

The first line of his proof would be

\(\tan^2\theta\cdot\cos^2\theta=\sin^2\theta\)

Well....with what I have done so far   f^-1 (-11)  = -2     

         Did I get something incredibly incorrect?  Am I going to be suspended? Ridiculed? Embarrassed?  Imprisoned?  Caned?  Beheaded?  ? 

Not sure why you are asking?  Hmmmmmm.......    

2.

We want to find the solutions to this system of equations:

y   =   2x² - 7x + 1

y   =   8x² + 5x + 1

8x² + 5x + 1   =   2x² - 7x + 1

                                                    Subtract  2x²  from both sides.

6x² + 5x + 1   =   -7x + 1

                                                    Add  7x  to both sides.

6x² + 12x + 1   =   1

                                                    Subtract  1  from both sides.

6x² + 12x   =   0

                                                    Factor  6x  out of both terms on the left side.

6x(x + 2)   =   0

                                                    Set each factor equal to zero.

6x  =  0     or     x + 2  =  0

x   =   0     or     x   =   -2

Using one of the equations, find  y  when  x = 0 .

When  x = 0 ,   y   =   2(0)² - 7(0) + 1   =   1

Find  y  when  x = -2 .

When  x = -2 ,   y   =   2(-2)² - 7(-2) + 1   =   8 + 14 + 1   =   23

The points of intersection are   (0, 1)   and   (-2, 23)

1.

x² - 10x + y² + 6y + c   =   0    Let's get this equation into standard form.

                                                Subtract  c  from both sides of the equation.

x² - 10x + y² + 6y   =   0 - c     Add  25  and  9  to both sides to complete the squares on the left.

x² - 10x + 25 + y² + 6y + 9   =   0 - c + 25 + 9      Factor each perfect square trinomial on the left.

(x - 5)²  +  (y + 3)²   =   0 - c + 25 + 9

(x - 5)²  +  (y + 3)²   =   -c + 34

Now that the equation is in this form, we can see that

(the radius)²  =  -c + 34        If the radius is  1 ,  then

1²   =   -c + 34

1   =   -c + 34

c  =  33