Hi Melody,
My jest was directed to EP, for his final (appended) remark, in the post above yours.
Purgatory is commonly regarded as a cleansing by way of painful temporal punishment, which, like the eternal punishment of h**l, is associated with the idea of fire. https://en.wikipedia.org/wiki/Purgatory#Pain_and_fire
Like any religious belief, individuals will adjust their viewpoints according to their own personality and perspective. So for many, such a place is an environment for prayer and meditation, while waiting for god to take them to heaven.
Personally, despite being raised as Catholic, I could never embrace any of the tenets of Catholicism (or any other religion). My first public demonstration of my contrary nature was in the fourth grade, after a visiting Brother gave a lecture (well couched in Catholic dogma) on creationism vs. evolution.
The teacher called on the students to ask questions or offer comments. Very few volunteered, so the teacher called on students individually. “Ginger, you usually have something to say.” I stood, which we were required to do when addressing the teacher or class, “You are too late,” I said. “I’ve already read Darwin’s book. God may have created the heavens and Earth, but I know I’m a chimp, just a new and improved version.”
After my comment, I started scurrying around the classroom and jumping on the tables while making chimp noises. I would have swung from the rafters if there were any. About a third of the class—mostly boys joined in the spectacle. I jumped on my best (boy) friend’s back; he could easily carry me around, and this continued for a few minutes, until the teacher scolded us back to our seats. During the commotion, I heard the Brother say to our teacher, “Your class room has become purgatory.” I remember thinking, “it may be purgatory for you, but it’s a little bit of heaven for us.”
Amazingly, we were not disciplined for this, although we did get a lecture on proper classroom behavior. After this, my classmates –usually boys– often brought me bananas. These banana gifts continued into high school. My chimp persona continues to this day.![]()
Sister Alice, my mathematics teacher for 7th, 8th, and the first half of 9th grade, would often “condemn” her students (sometimes individually) to additional time in purgatory for poor math scores on tests. Her comments never came across as any kind of jest or levity. I would often intentionally “solve” problems incorrectly using various absurd methods, just to listen to her howl. My math grades were poor anyway, and by doing this, I rarely scored higher than D’s.
After one particular midterm exam, Sister Alice returned my test, saying, “Ginger, you are not going to purgatory, you’re going straight to heII!” To which I replied, “Oh, I’ll keep your company then, and you can teach me the correct way to solve these.”
My class thought this was funny, but Sister Alice didn’t. I received an immediate detention—the parochial school’s version of purgatory. I spent the time drawing Sister Alice roasting in heII, with demons stabbing her with pitchforks, inscribed with errant mathematical equations. I titled it Saint Alice Skips Purgatory.
Sister Alice was also the art teacher for the secondary grades, and she never cared much for my art, despite the fact that at least one of my art works always received honorable mention in every regional completion I entered—including one titled Beyond Purgatory, based on the one I did in detention. The Mother Superior (principal) confiscated the original—not because of the subject matter, but because detention was supposed to be a time of repentance and meditation. When she confiscated my drawing, she was doing her best to suppress her laughter.
The Mother Superior was usually “no nonsense” when it came to running the school, but she did have a sense of humor. Years later, after her funeral mass, someone told me she had my drawing framed, and she would hang it in her quarters for the week preceding All Saints' Day (Halloween).
To me this honor far exceeded all the gold/blue, silver/red, and bronze/white ribbons I’d won for any art completion.![]()
GA
I think this is one of those times where simplifying the problem may make it easier to understand. Mathematicians utilize this strategy all the time, and it amazes me how many times it works. Instead of considering a three-dimensional figure, let's solely focus on the base of the tetrahedron, figure PQR.
A few rules govern the existence of this triangle. Let's consider the rules one at a time. If the sidelengths of \(\triangle PQR\) can only consist of lengths of 18 or 41, then this narrows the possibilities to 4 options. The images below are not drawn to scale. The central label indicates how I will differentiate and refer to the triangles:
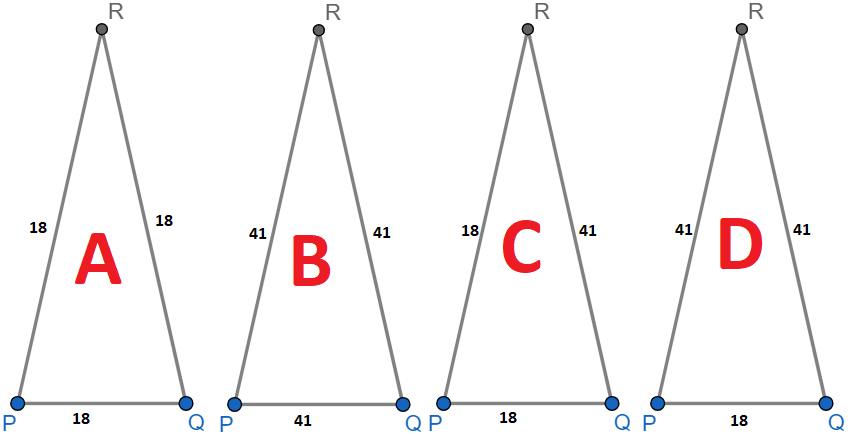
The next rule is that no face is equilateral; in other words, the triangle cannot have all sides with equal length. Since both triangle A and triangle B are equilateral in nature, these two cannot be the base of the tetrahedron.
There are no more rules given in the problem, yet there are still two triangles left as possibilities. Can we eliminate one? Yes, absolutely! Triangle C cannot be a triangle because it cannot exist. By the Triangle Inequality Theorem, the sum of the lengths of any two sides of a triangle must be greater than the length of the remaining side. The triangle fails this theorem. \(18+18\ngtr 41\). If a triangle fails the theorem, then the figure cannot be a triangle.
This leaves us with one and only one possibility: the 18-41-41 triangle. Since all the faces of this figure, known as a tetrahedron, is a triangle with the rules aforementioned, then all other faces must be an 18-41-41 triangle, too. A tetrahedron has 4 faces, so I can find the area of one base and multiply it by 4. The area of the base can be obtained with heron's formula. Doing this will get the surface area of the three-dimensional figure.
| \(SA_{\text{tetrahedron}}=4\sqrt{s(s-a)(s-b)(s-c)}\) | In heron's formula, a, b, and c are side lengths of any triangle. s is the semiperimeter. Let's find the semiperimeter first. |
| \(s=\frac{18+41+41}{2}=50\\ a=18\\ b=41\\ c=41\) | Now, substitute into heron's formula and solve. |
| \(SA_{\text{tetrahedron}}=4\sqrt{50(50-18)(50-41)(50-41)}\) | Simplify the expressions within parentheses. |
| \(SA_{\text{tetrahedron}}=4\sqrt{\textcolor{red}{50}*\textcolor{blue}{32}*\textcolor{green}{9*9}}\) | Let's try to extract all the perfect squares from this. |
| \(SA_{\text{tetrahedron}}=4\sqrt{\textcolor{red}{25*2}*\textcolor{blue}{16*2}*\textcolor{green}{9^2}}\) | We can combine the red 2 with the blue 2 to make another perfect square. |
| \(SA_{\text{tetrahedron}}=4\sqrt{5^2*4^2*9^2*2^2}\) | Let's take out all the perfect squares now! |
| \(SA_{\text{tetrahedron}}=4*\textcolor{red}{5*4}*\textcolor{blue}{9*2}\) | Now, multiply in any order you choose. I chose to multiply this way because it felt easiest. |
| \(SA_{\text{tetrahedron}}=\textcolor{red}{4}*20*\textcolor{red}{18}\) | |
| \(SA_{\text{tetrahedron}}=20*72\) | |
| \(SA_{\text{tetrahedron}}=1440\text{units}^2\) | Do not forget about those units! |