All Answers 358925 Answers

216/[5+7+12]=9 value of 1 unit
9 x 5 = 45 small cakes sold
9 x 7 =63 medium cakes sold
9 x 12 =108 large cakes sold.
Let the profit on 1 small cake =p, then:
45p + 63*2p + 108*3p =648.45, solve for p
p = 1.31 pounds - profit on 1 small cake.

If the roots of the quadratic equation \(\frac12x^2+99x+c=0 \) are \(x=-99+\sqrt{8001}\) and \(x=-99-\sqrt{8001},\) then what is the value of \(c\)?

\(c=\boxed{900}\)

I hope this helped,

Gavin

You could also do it this way:

5 = (x³ - 2x² -8x)/(x + 2)

5 = x(x + 2)(x - 4)/(x+2)

5 = x(x - 4)

x² - 4x - 5 = 0

(x + 1)(x - 5) = 0

x = -1 or x = 5

1: 

The line 

\(y = (3x + 7)/4 \)

y = (3x + 7)/4

intersects the circle

\(x^2 + y^2 = 25 \)

x^2 + y^2 = 25

at A and B.

Find the length of chord .

\(\begin{array}{|rcll|} \hline x^2+y^2 &=& 25 \quad & | \quad y = \dfrac{3x+7}{4} \\ x^2+ \left(\dfrac{3x+7}{4}\right)^2 &=& 25 \\\\ x^2+ \dfrac{(3x+7)^2}{16} &=& 25 \quad & | \quad \cdot 16 \\\\ 16x^2+ (3x+7)^2 &=& 25\cdot 16 \\ 16x^2+ (3x+7)^2 &=& 400 \\ 16x^2+ 9x^2+42x + 49 &=& 400 \\ 25x^2+42x + 49-400 &=& 0 \\ 25x^2+42x - 351 &=& 0 \\ x &=& \dfrac{-42\pm \sqrt{42^2-4\cdot 25\cdot(-351) } } {2\cdot 25} \\\\ x &=& \dfrac{-42\pm \sqrt{1764+100\cdot(351) } } {50} \\\\ x &=& \dfrac{-42\pm \sqrt{36864} } {50} \\\\ x &=& \dfrac{-42\pm 192} {50} \\\\ x_a & =& \dfrac{-42 + 192} {50} \\ \mathbf{x_a} &\mathbf{=}& \mathbf{3} \\ y_a &=& \dfrac{3\cdot 3+7}{4} \\ \mathbf{y_a} & \mathbf{=}& \mathbf{ 4 } \\\\ \mathbf{x_b} & \mathbf{=}& \mathbf{\dfrac{-42 - 192} {50} } \\ x_b &=& -4.68 \\ y_b &=& \dfrac{3\cdot (-4.68)+7}{4} \\ \mathbf{y_b} & \mathbf{=}& \mathbf{-1.76} \\ \hline \end{array}\)

The length of chord AB:

\(\begin{array}{|rcll|} \hline && \sqrt{(x_a-x_b)^2+(y_a-y_b)^2} \\ &=& \sqrt{[3-(-4.68)]^2+[4-(-1.76)]^2} \\ &=& \sqrt{(3+4.68)^2+(4+1.76)^2} \\ &=& \sqrt{7.68^2+5.76^2} \\ &=& \sqrt{92.16} \\ &=& 9.6 \\ \hline \end{array}\)

The length of chord AB is 9.6

We can model the rate of a change as a right triangle with base \(x = 400\) feet and height y increasing at a rate of 10 feet per second.

After 30 seconds, \(y=10\cdot30=300\)

If the distance between Eric and Harrison is z, the Pythagorean Theorem gives us: \(z^2 = x^2 + y^2 \).

The distance between Eric and Harrison is: \(x^2=300^2+400^2\Rightarrow x=500\)

Differentiating both sides also yields \(2z · z' = 2x · x' + 2y · y'\). Plugging in our values, we get \(2 · 500z' = 2 · 400 · 0 + 2 · 300 · 10\), which gives us \( z' = 6\) feet per second.

I hope this helped,

Gavin

When the rectangle perfectly covers the curved surface of the cylinder without overlapping itself at all, the length of the rectangle forms a circle that the the base of the cylinder. 

When we know the area of the base of the cylinder, we can multiply it by the height to find the volume. 

Since the length of the rectangle is 24, the radius of the circle is \(\frac{12}{\pi}\). 

The area is: 

\((\frac{12}{\pi})^2\cdot\pi=\frac{144}{\pi}\)

The volume is \(144\cdot8\div\pi\)

I hope this helped,

Gavin

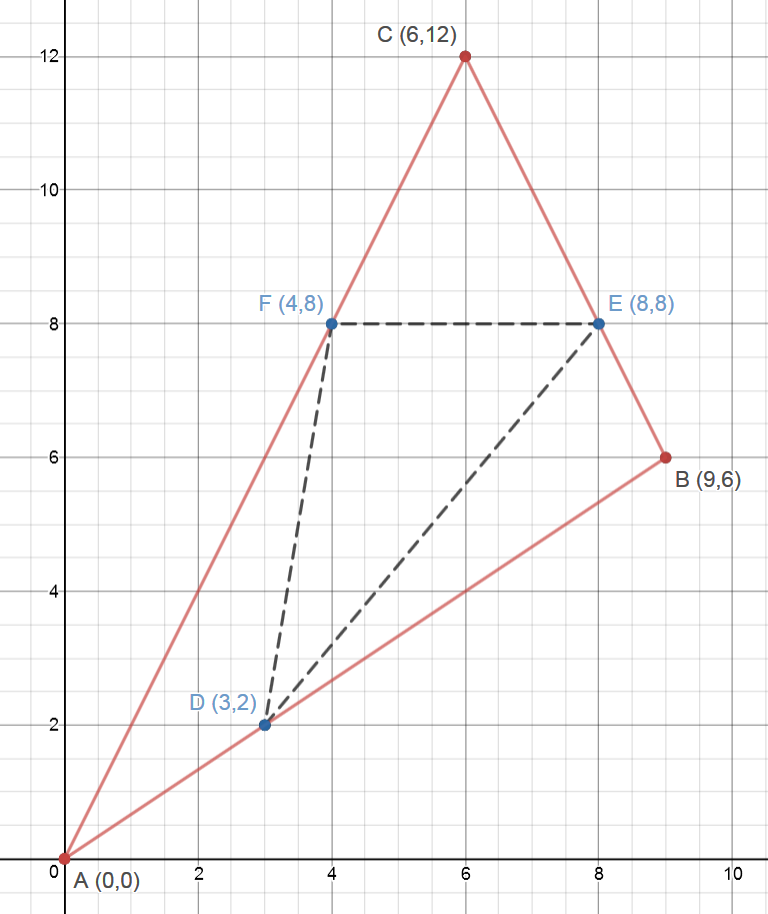
2:  Points A(0,0), B(9,6) and C(6,12) are vertices of triangle ABC.
Point D is on segment AB such that 2(AD) = DB,
point E is on segment BC such that 2(BE) = EC and
point F is on segment CA such that 2(CF) = FA.
What is the ratio of the area of triangle DEF to the area of triangle ABC?
Express your answer as a common fraction.

\(\begin{array}{|rcll|} \hline D &=& \dbinom{9}{6}\cdot \dfrac13 \\ &=& \dbinom{3}{2} \\\\ E &=& \dbinom{9}{6} + \left( \dbinom{6}{12} - \dbinom{9}{6} \right)\cdot \dfrac13 \\ &=& \dbinom{9}{6} + \dbinom{-3}{6}\cdot \dfrac13 \\ &=& \dbinom{9}{6} + \dbinom{-1}{2} \\ &=& \dbinom{8}{8} \\\\ F &=& \dbinom{6}{12}\cdot \dfrac23 \\ &=& \dbinom{12}{24}\cdot \dfrac13 \\ &=& \dbinom{4}{8} \\ \hline \end{array} \\ \begin{array}{|rcll|} \hline \text{Area}_\text{ABC} &=& \frac12 \left( 0\cdot 6 - 9\cdot 0 + 9 \cdot 12 - 6 \cdot 6 + 6\cdot 0 - 0 \cdot 12 \right) \\ &=& \frac12 \left( 9 \cdot 12 - 6 \cdot 6 \right) \\ &=& \frac12 \left( 72 \right) \\ &=& 36 \\ \hline \end{array} \\ \begin{array}{|rcll|} \hline \text{Area}_\text{DEF} &=& \frac12 \left( 3\cdot 8 - 8 \cdot 2 + 8 \cdot 8 - 4 \cdot 8 + 4\cdot 2 - 3 \cdot 8 \right) \\ &=& \frac12 \left( 24-16+64-32+8-24 \right) \\ &=& \frac12 \left( 24 \right) \\ &=& 12 \\ \hline \end{array}\\ \begin{array}{|rcll|} \hline \dfrac { \text{Area}_\text{DEF} } {\text{Area}_\text{ABC}} &=& \dfrac{12}{36} = \dfrac13 \\ \hline \end{array}\)

If the underscore is supposed to be a minus sign then, 
\((b-a)^2=71-a\)

Since b = a-1, we can substitute the b in the first equation with a-1.
Then, we solve for a.

\((b-a)^2=71-a\\ (a-1-a)^2=71-a\\ (-1)^2=71-a\\ 1=71-a\\ a=70\)

-2 doens't work because that would make the denominater zero, but other than that, thanks for the help!

If this is what you mean, then:

(500 nPr 400)/(500 nPr 100)*(1/400 nPr 300) =1

simplify | ((500!)/((500 - 400)!))/((500!)/((500 - 100)!))×1/((400!)/((400 - 300)!))
=(500!/(500-400)! x (500-100)!/500!=(100!*400!) * 1/(400!)*(100!)
=(100!*400!) / (100!*400!) =1

16x^(4) -96x^(3)y +216x^(2)y^(2) -216xy^(3) +81y^(4)

=(2x - 3y)^4

Solve for x:
5 x + 10 = x^3 - 2 x^2 - 8 x

Subtract x^3 - 2 x^2 - 8 x from both sides:
-x^3 + 2 x^2 + 13 x + 10 = 0

The left hand side factors into a product with four terms:
-(x - 5) (x + 1) (x + 2) = 0

Multiply both sides by -1:
(x - 5) (x + 1) (x + 2) = 0

Split into three equations:
x - 5 = 0 or x + 1 = 0 or x + 2 = 0

Add 5 to both sides:
x = 5 or x + 1 = 0 or x + 2 = 0

Subtract 1 from both sides:
x = 5 or x = -1 or x + 2 = 0
Subtract 2 from both sides:

x = 5    or     x = -1     or      x = -2

\(12x^2+99x+c=0\)

\(x = -99\pm\sqrt{8001}\)

I think you have written the question wrong. I think both those answers are suppposed to be over 24.

If the roots of the quadratic equation \(12x^2+99x+c=0\) are \(x = -99+\sqrt{8001}\) and \(x=-99-\sqrt{8001}\), then what is the value of \(c\)?

Can somebody translate this into proper LaTex?

The length of Q = 40 x 1.25 =50

The area of Q =50y cm^2

The area of P =40x cm^2

40x * 0.90 = 50y

36x = 50y, solve for x/y

x/y = 50 / 36 =25 / 18

So, the ratio of x : y =25 : 18. This does make sense because:

Area of P =40 x 25 =1,000 cm^2, and:

Area of Q =50 x 18 =900 cm^2 - which is 90% of area of P.

1m³ concrete = 2400 kg

Find the weight w/o water.
2400 * 0.85 = 2040 kg

1 cement:2 sand:5 stone
8 total parts
2040/8 = 255 kg
Each part is 255 kg.

Cement: 1 part = 255kg
Sand: 2 parts = 255*2 = 510kg
Stone: 5 parts = 1275kg

a) Angle XBC = 55^o because it corresponds with Angle AXY.
b) Since Angle XBC = 55^o, XCB = 55^o
[If two sides of a triangle are congruent, then the angles opposite to them are congruent.]
180-55-55 = 70

[Angles in a triangle add up to 180.]

Angle BXC = 70^o

x = 0.11111111...
10x = 1.11111111...
10x-x = 1.1111111111...-0.111111111...
9x=1
x=1/9

y = 0.0101010101...
100y = 1.0101010101010...
100y-y = 1.01010101010...-0.01010101010101...
99y = 1
y = 1/99

z = 0.0001000100010001...
10000z = 1.000100010001...
10000z-z = 1.000100010001...-0.000100010001...
9999z = 1
z = 1/9999

\(x+y+z\\ \frac{1}{9}+\frac{1}{99}+\frac{1}{9999}\\ \frac{1111}{9999}+\frac{101}{9999}+\frac{1}{9999}\\ \frac{1213}{9999} \)

 

Take the reciprocal of each:

0.11111111111 =1/9

0.01010101010 =1/99

0.000100010001 =1/9999

1/9 + 1/99 + 1/9999 =1213/9999

f(1) = 120

f(1+1) = -0.5f(1) = -0.5*120 = -60

f(2+1) = -0.5f(2) = -0.5*-60 = 30

f(3+1) = -0.5f(3) = -0.5*30 = -15

f(4+1) = -0.5f(4) = -0.5*-15 = 7.5

So, f(5)=7.5

Here's my solution to it, I've only self taught myself so don't mind the inefficiency of it