All Answers 356405 Answers

OK.....you do not seem to be learning any of this material.....many of your many questions are very similar and require similar thinking and formulas.....TRY to get an answer THEN ask for help.....

Triangle area = 1/2 base * height      You SHOULD be able to answer the question with this bit of info....TRY!  You learn NOTHING by only looking for answers!

L = 6 + w    given

Perimeter = 2 * L + 2 * W

2 (6+w) + 2w = 72

12 + 2w + 2w = 72

4w = 60

w=15        L = 6+w = 21

VERTICALLY stretching the graph means INCREASING the amplitude.....multiply the graph by 4     Second choice.

1.
Let z be a complex number such that \(|z - 12| + |z - 5i| = 13\).
Find the smallest possible value of \(|z|\).

\(\text{Let $z=a+bi$ } \\ \text{Let $|z|=\sqrt{a^2+b^2}$ } \)

\(\begin{array}{|rcll|} \hline z - 12 &=& a+bi - 12 \\ &=&(a-12) +bi \\ |z-12| &=& \sqrt{(a-12)^2+b^2 } \\ \hline z - 5i &=& a+bi - 5i \\ &=& a + (b-5)i \\ |z - 5i| &=& \sqrt{a^2+(b-5)^2} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \mathbf{|z - 12| + |z - 5i|} & \mathbf{=}& \mathbf{13} \\\\ \sqrt{(a-12)^2+b^2 } + \sqrt{a^2+(b-5)^2} &=& 13 \\ \sqrt{(a-12)^2+b^2 } &=& 13- \sqrt{a^2+(b-5)^2} \quad | \quad \text{square both sides} \\ (a-12)^2+b^2 &=& \left( 13- \sqrt{a^2+(b-5)^2} \right)^2 \\ (a-12)^2+b^2 &=& 13^2-26\sqrt{a^2+(b-5)^2}+ a^2+(b-5)^2 \\ 26\sqrt{a^2+(b-5)^2} &=& 13^2+ a^2+(b-5)^2-(a-12)^2-b^2 \\ 26\sqrt{a^2+(b-5)^2} &=& 13^2+ a^2+b^2-10b+25-b^2-a^2+24a-12^2 \\ 26\sqrt{a^2+(b-5)^2} &=& 13^2+ -10b+25+24a-12^2 \quad | \quad 13^2-12^2 = 5^2=25 \\ 26\sqrt{a^2+(b-5)^2} &=& 50 -10b +24a \quad | \quad : 2 \\ 13\sqrt{a^2+(b-5)^2} &=& 25 -5b +12a \quad | \quad \text{square both sides} \\ 13^2\left(a^2+(b-5)^2\right) &=& (25-5b+12a)^2 \\ 13^2\left(a^2+(b-5)^2\right) &=& 25^2+25b^2+12^2a^2-250b+24\cdot 25a-120ab \\ 13^2a^2+13^2(b-5)^2 &=& 25^2+25b^2+12^2a^2-250b+24\cdot 25a-120ab \\ 13^2a^2+13^2(b^2-10b+25) &=& 25^2+25b^2+12^2a^2-250b+24\cdot 25a-120ab \\ 13^2a^2+13^2b^2-13^2\cdot 10b+13^2\cdot 25 &=& 25^2+25b^2+12^2a^2-250b+24\cdot 25a-120ab \\ (13^2-12^2)a^2+(13^2-5^2)b^2+13^2\cdot 25 &=& (13^2\cdot 10-250)b+600a-120ab+25^2-13^2\cdot 25 \\ 5^2a^2+12^2b^2&=& 1440b+600a-120ab-3600 \\ (5^2a^2+120ab+12^2b^2) &=& 120(5a+12b)-3600 \\ (5a+12b)^2 &=& 120(5a+12b)-3600 \\ \hline \end{array} \)

\(\begin{array}{|rcll|} \hline (5a+12b)^2 &=& 120(5a+12b)-3600 \\ (5a+12b)^2 -120(5a+12b)+3600 &=& 0 \\\\ 5a+12b &=& \dfrac{120\pm \sqrt{120^2-4\cdot 3600}}{2} \\ 5a+12b &=& \dfrac{120\pm 0}{2} \\ 5a+12b &=& \dfrac{120}{2} \\ \mathbf{ 5a+12b } &\mathbf{=}& \mathbf{60} \quad \text{this is a line!!! }\\ \text{or}\quad b&=&5-\dfrac{5}{12}a \\ \hline \end{array} \)

The normal vector of this line \(5a+12b-60=0\), perpendicular to the line is \(\vec{n}=\dbinom{5}{12}\)

\(\begin{array}{|rcll|} \hline \vec{n_0} &=& \dfrac{1}{\sqrt{5^2+12^2}} \dbinom{5}{12} \\\\ &=& \dfrac{1}{\sqrt{13^2}} \dbinom{5}{12} \\\\ &=& \dfrac{1}{13} \dbinom{5}{12} \\\\ &=& \begin{pmatrix} \dfrac{5}{13}\\ \dfrac{12}{13} \end{pmatrix} \\\\ |z|_{\text{min}} &=& \dbinom{0}{5}\cdot \begin{pmatrix} \dfrac{5}{13}\\ \dfrac{12}{13} \end{pmatrix} \\ &=& 0\cdot\dfrac{5}{13}+5\cdot \dfrac{12}{13} \\\\ & = & \dfrac{5\cdot 12}{13} \\\\ & = & \dfrac{60}{13} \\\\ \mathbf{ |z|_{\text{min}} } & \mathbf{=} & \mathbf{4.61538461538} \\ \hline \end{array}\)

The smallest possible value of |z| is 4.61538461538

A water trough is 7 m long and has a cross-section in the shape of an isosceles trapezoid that is 30 cm wide at the bottom, 80 cm wide at the top, and has height 50 cm. If the trough is being filled with water at the rate of 0.3 m3/min how fast is the water level rising when the water is 40 cm deep?

I am going to refer to depth as height (h).  It is much less confusing than d would be.

We are given the dimensions of the trough and we are given    \(\frac{dV}{dt}\\ \)

We are asked to find  \(\frac{dh}{dt}\)   when h = 0.4 metres.

Now

     \(\frac{dh}{dt}=\frac{dh}{dV}\times \frac{dV }{dt}\\ \frac{dh}{dt}=\frac{dh}{dV}\times 0.3\\\)

So can I find   dh/dV?  

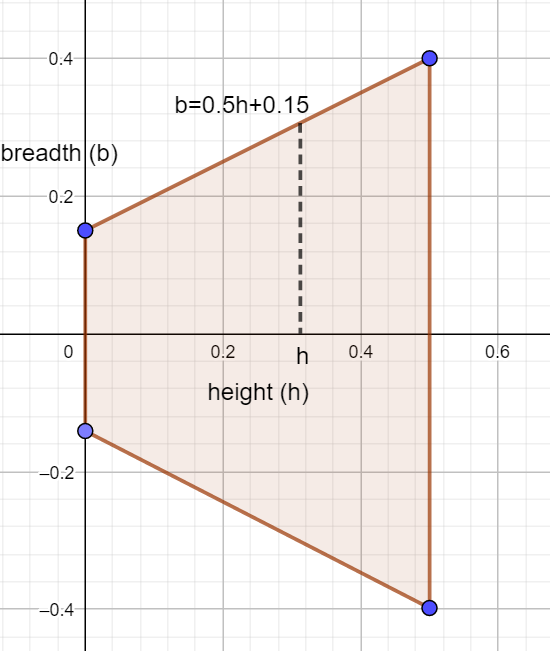
The pic shows the area cross section of the trough.   (it is sideways)

Presenting it like this it was easy to find that the eqation of the side is b=0.5h+0.15    

For any specific height h the surface area is a rectangle.  the length is 7m,  the breadth is   2(0.5h+0.15)

So the surface area is

\(S=7*2(0.5h+0.15)\\ S=7h+2.1\\~\\\)

\(Volume\\ V=\frac{1}{2}*2*(0.15+\frac{h}{2}+0.15)*h*7\\ V=(0.3+\frac{h}{2})*7h\\ V=2.1h+\frac{7h^2}{2}\\ \\~\\ \frac{dV}{dh}=7h+2.1\\ \frac{dh}{dV}=\frac{1}{7h+2.1}\\~\\ when\;\;h=0.4m\\ \frac{dh}{dV}=\frac{1}{7*0.4+2.1}=\frac{1}{4.9}=\frac{10}{49}\\\)

\(\frac{dh}{dt}=\frac{dh}{dV}\times \frac{dV }{dt}\\ \frac{dh}{dt}=\frac{10}{49}\times 0.3\\ \frac{dh}{dt}=\frac{3}{49} \; m/s\\\)

At the instant when the water is 0.4 metres deep the water is rising at     \(\frac{3}{49}\;\;m/sec\)

This could easily be riddles with errors, you had best check it very carefully.

Emerald Wonder, if you want to answer physics questions (or any type of applied mathematics), you should demonstrate the application of the relevant equations, including the proper use of units. Plopping half-hearted, unintelligible bullshit along with a wrong answer is not a substitute. 

\(\bf \Large \beta \small \left(dB\right) \large =10\log_{10}\left(\frac{I}{I_0}\right) ~ | ~ \bf \tiny \text {(β) = sound intensity level in decibels; (I) = intensity in watts per meter squared; } I_0 \text { = standard corresponding to zero (0) decibels. }\\\\ \small \dfrac{20W}{10m^2} =\dfrac{2W}{m^2} \quad | \quad \bf \tiny \text {Convert point source area of sound to standardized area of one (1) square meter. }\\ 10\log_{10}\left(\frac{2W\cdot m^{-2}}{10^{-12}W\cdot m^{-2}}\right) = 123 ~ \small \bf dB \normalsize \quad | \quad \tiny (10^{-12}W \cdot m^{-2}) \text { -standard zero (0) decibel reference. }\\ \)

GA

Do you know what the answer is to this question?

I know you want to know how to do it, I am just wondering if you are given the final answer.

The population at the end of the n'th year is p = 15000*(1.065)ⁿ    (assuming 15000 is the population at the beginning of the first year).

You should be able to graph this on a graphing calculator.

The following should help:

If y(x) = atan(k/x) where k is a constant, then dy/dx = -k/(k² + x²)