The following presentation is adapted from conversational dialogues with Lancelot Link for stochastic measurement errors in the physical sciences.
------------------
To calculate the error range for uncorrelated and random errors, use Gauss’s equations for normal distribution of errors. Using the Gauss equations, gives a 68% confidence interval the measurement error is within this range.
Here are some basic derivatives from the Gauss equations:
\(\small \text{If Q is a combination of sums and/or differences, then the sigma (error) of Q is equal to } \\ \sigma Q = \sqrt{(\sigma a)^2 + (\sigma b)^2 . . . + (\sigma x)^2 . . . } \\ \text{If } Q = b^2 \text{ then } \sigma Q = 2(\sigma (b)) \text{ where } \sigma (b) \text{ is the error of (b)}\\ \text{If } Q = \sqrt{(b)} \text{ then }\sigma Q = \frac{1}{2} (\sigma (b)) \text{ where } \sigma (b) \text{ is the error of (b)}\\ \text{Note how the exponent becomes the multiplier of the error.}\\ \small \text {For this equation, the easiest method is to calculate each error as a }\\ \small \text {decimal and then use the sum of the decimals to calculate the error range. }\\ \text {Uncertainties (In decimal) for a, b, and c. }\\ a_1 = \frac{0.1}{1.3} = 0.0769\\ b_1 = (2)\frac{0.2}{2.8} = 0.1428\\ c_1 = (0.5)\frac{0.1}{0.8} = 0.0625\\ Q= \frac{1.3 \times (2.8)^2}{\sqrt {0.8}} = 11.4 \pm ((0.0769 + 0.1428+ 0.0625) * (11.4))\\ Q= 11.4 \pm 3.2 \\ \small \text { note: pay attention to significant figures when recording the final error range. }\\ \\\)
-----------------------
Relating to this question and others you’ve posted on here , another important thing you need to do is Stop being a lazy dolt!
I would have answered your chemistry questions, except I was too lazy. I caught this laziness from you—it’s more contagious than dumbness.![]()
GA
Here is a diagram for you to reference as I solve for the area of the triangle. Notice that I added \(\overline{FG}\) such that the segment is the altitude of the triangle.
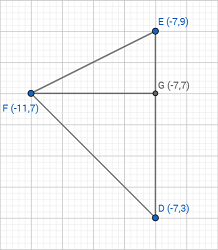
Since the altitude and base of this triangle lie on gridlines, we can simply count the distance (as opposed to using the distance formula).
\(ED=6\\ FG=4\)
We already have all the information needed to solve for the area. Just use the area formula for a triangle, A=1/2*bh.
| \(A_{\triangle DEF}=\frac{1}{2}ED*FG\) | We already know the values of ED and FG, so let's plug them in! |
| \(A_{\triangle DEF}=\frac{1}{2}*6*4\) | Now, we simplify. multiplying 6 by 1/2 eliminate the fraction, but you can multiply in any order you'd like. |
| \(A_{\triangle DEF}=3*4\) | |
| \(A_{\triangle DEF}=12\text{units}^2\) | |